Last Updated on August 6, 2025 by Maged kamel
The inverse of a Matrix-inverse of a 2×2 matrix.
A brief description of the content of the lecture.
The objective of this lecture is to determine the inverse of a matrix by elementary row operation and use it for solving the simultaneous equation by lower/upper factorization or Doolittle’s factorization for the lower /upper factorization. How can we use elementary matrices to get the inverse of a 2×2 matrix?

How to find the inverse of a matrix?
First, let us discuss how to get the inverse of a matrix by using elementary operations, we are using the Augmented matrix on the left-hand side will be written a matrix denoted by A, separated by a line and this is the identity matrix I.
For example, it is 3 by 3 or 2 by 2 or 4 by 4, and it’s written in the capital letter L.
Through elementary operations, we are converting our original matrix A to the identity matrix I, and through the elementary operations, the I, which was in the augmented matrix on the right-hand side of the Augmented matrix, will be converted into A-1, where A-1 is the inverse of A.
Our original matrix, which is the one we are looking for, what are the set of elementary row operations.
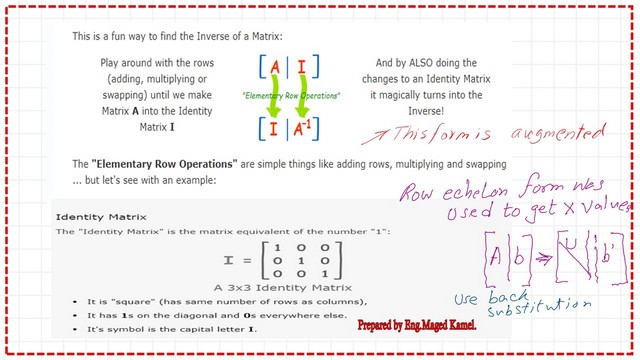
The possible operations on a matrix.
There are three operations: one is the swap of rows, changing from R1 to R2, which changes the location; another is multiplying or dividing each element in the row by a constant.
The 3rd of operation is replacing rows by adding or subtracting multiple other rows. We can say R1 +2*R2 or R1-R3 where R1 is the first-row donation and R3 is the third row, etc.

A solved example of how to get the inverse of a matrix of a 2×2 matrix?
For example, if we have a matrix that is 2×2, it’s required to find the inverse of a 2×2 matrix where A (-3 -2, 7 4), respectively.
The solution that we are going to use is the augmented matrix; we write on the left-hand side our matrix A.
We divide the matrix by a vertical line, and we are putting the identity matrix. In our case, it will be 2 by 2. The diagonal, as we can see, is (1 and 1), and the other elements are zeros.
We want to convert the left-hand side into (1 1 0 0). How can this be done?
First, to make -3 converted to +1, we multiply R1*1/3, and the result we are going to put in the place of R1, so this (-3*-1/3) to 1,(-2*-1/3), it will give us (+2/3), and the right-hand side will be (-1/3,0).
While the second row will be left unchanged because there is no operation, it will move the same elements, which are a (7 4 0 1) here.
The next step will be making this 7 = 0 and this can be done by multiplying the first row by(-7) and adding to the second row R2, so (-7*1+7) will become 0, here 2/ 3 -7 +4=-2/3, -7*-1/3 will be 7/3 and the application of 0 will be 0 + R2.
The next step is to multiply the second row by (-3/2) and place it in our table to zero, which is the same. This is reciprocal, which would become 1 and 7/3 RI.(-3/2) It will become (-7/3) -3/2 or the last item, which is equal to 1.

The next target is to make 2/3 =0, this can be done by multiplying the second row, which is 1, by -2/3, and adding to 1.
We get (1 0 2 +1 ), and since the second row is unchanged, it will be maintained at ( 0 1 – /2 (-3/2). On the left-hand side, we find that the diagonal is 1 and the other diagonal is 0.
This is the inverse we are looking for; it is divided and lies in the right-hand portion of this line.
Another way to get the inverse of a matrix is by using the determinant.
There is a rule for the matrix A if it is (2×2), we replace this, we swap these -3 will go down, while we are going to change the sign of 7, it will become -7, and the -2 will become the +2.
But again we are going to divide on the determinant which is(-3*4-1*-2), which at the end will become +2, so the inverse of the matrix is called adjoint divided by the determinant, the adjoint is (4 -2, and (-7 -3/2). The details of the operations can be seen in the next slide image.

The result we obtained by using the determinant is identical to the result obtained by the augmented matrix.
Introduction to Elementary Matrices.
The following slide image explains the definition of an Elementary matrix. There are three types of these matrices: the first one is E1, which is obtained by swapping rows of an Identity matrix. The second one is E2, which is obtained by multiplying a row of the identity matrix by a non-zero constant.
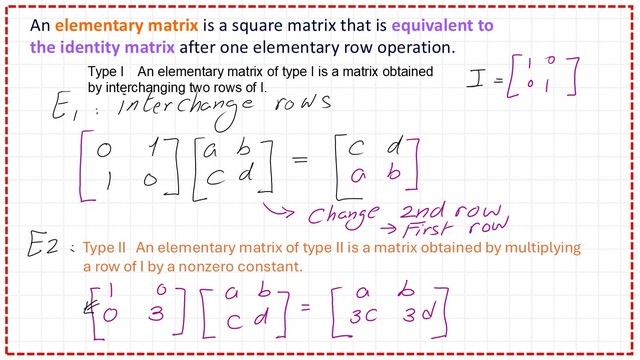
The third elementary matrix is E3, which is obtained from an Identity matrix by adding a multiple of one row to another row.

Find the inverse of a matrix by elementary matrices.
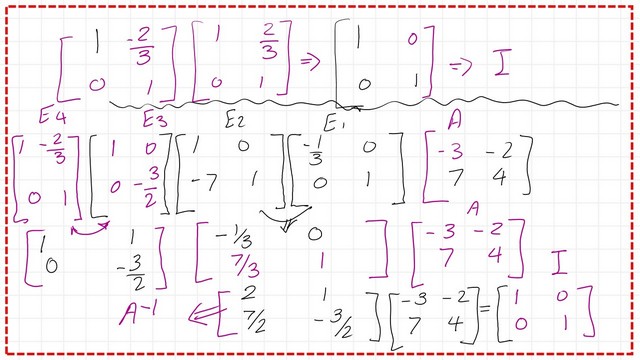
For the same example, we have used to get the inverse of a matrix, we will perform the same operations on matrix A, but by using elementary matrices. The first operation was multiplying the first row by(-1/3) and placing the result in the same row. This can be done by multiplying Matrix A by (-1/3 0, 0 1), which is type E1.

The second operation was multiplying the first row by(-7) and adding to the second row, and placing the result in the second row. This can be done by multiplying the product of Matrix A by E1, with another elementary matrix that is (1 0, -7 1). This matrix is the E2 matrix. Please refer to the next slide image for illustration.

The third operation was multiplying the second row by(-3/2), and placing the result in the second row. This can be done by using another elementary matrix E3. The last operation by multiplying (-2/3) by the second row and adding to the first row. The result is placed in row 1; this is done by using the E4 elementary matrix. Please refer to the next slide image for illustration.

To get the inverse of matrix A, we will use the four types of elementary matrices. By multiplying E4*E3*E2*E1, the result is the inverse matrix. To check that we have the correct solution, we multiply by A, and we get the identity matrix.
If we multiply the inverses of E1, E2, E3, and E4 by the identity matrix, we get the value of the A matrix. Thanks a lot.
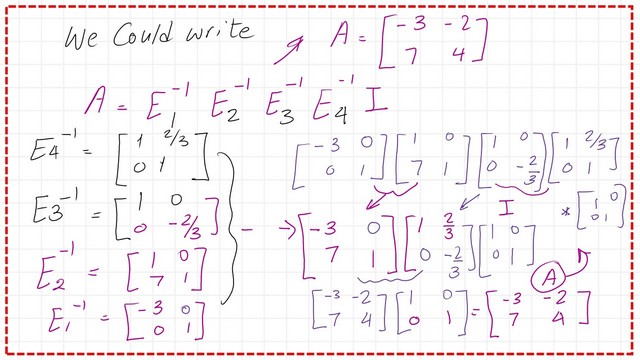
The next post is an Easy Illustration of the LU decomposition method for a 2×2 matrix.
HELM-Helping Engineers Learn Mathematics.
This is the Omni calculator for estimating various items of linear algebra -LU Decomposition Calculator.
This is a link to another –Calculator for matrices.
