Last Updated on February 5, 2026 by Maged kamel
Collapse Load For A Simply Supported Beam.
A solved problem for the collapse load for a simply supported beam under concentrated load.
We continue the discussion of the plastic theory, for the viewers, for the first time, refer to the two videos civil 120-8 and civil120-9 to take an idea regarding the plastic theory.

We have a simply supported beam with a hinged support at joint A and a roller support at B. The beam carries a concentrated load P at the midpoint of the span, and the span length is L. The following slide image shows the definitions of the yield load and Plastic load.

It is necessary to estimate the beam’s collapse load. Due to the beam’s collapse, a plastic hinge forms; it is then necessary to estimate its length.
To create a mechanism, we need to check the beam in question. Check the degree of indeterminacy, then add 1 to develop a mechanism for collapse in which the beam will collapse.
We have two reactions at the hinged support, and the reaction at the roller support equals 1, 2 + 1 = 3. We have three degrees of equilibrium equations; then, subtract the equilibrium equations from the total reactions, 3-3=0.
We need to convert the beam from a statically determined Stable system to an unstable beam to create the mechanism of collapse by providing an additional hinge.
The suggested place to add the hinge is at the load location, where the maximum moment occurs.
At the Midpoint of the span, when the load P gradually increases from zero to Py. As a reminder, the reaction at both supports is P/2, and the bending moment at L/2 =P*L/4.

In the diagram of the bending moment, this is the moment at point c, Mc=P*L/4 which is < My, when P=Py, M at c=Py*L/4. For a further increase in load on P plastic, the moment at point c will be Pp*L/4.
If we refer to the strain stress relationship, the stress can be represented by a linear relation, where the uppermost fibre will have a stress =Fy.
For the second stage, the stress becomes elastic-plastic; the stress at the top is Fy, and part of the upper fiber stress will be increased to Fy. At the last stage, the stress in the whole section is equal to Fy.

How to estimate the Collapse load for the beam?
In the section shown, at point c, where the plastic hinge forms, the top fibre is stressed to Fy; it cannot carry any more stress as the load increases. A further increase of load will cause the lower fiber to be stressed to Fy at that point, the stress =Fy, a hinge is formed. At the hinge, there will be a moment M on both sides.
This is the mechanism of failure where the moment reaches Mp. The plastic moment value is Mp = Pp*L/4 when the load is Pp. When the load is Pp = 4*(Mp/L), the section is in the plastic region.
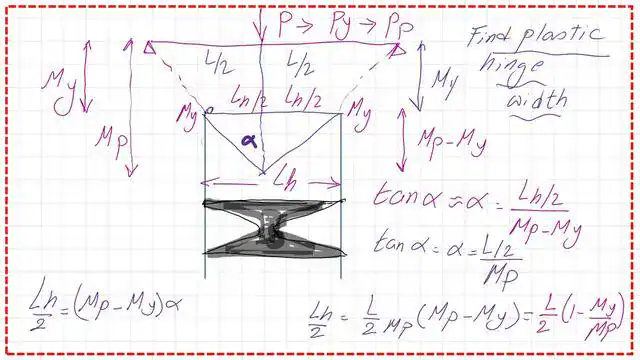
How to estimate the length of the plastic hinge?
If we place the hinge section below the bending moment diagram. In the following diagram, the moment of a zero-stiffness hinge at Mp is shown; the hinge is centred at 0.
Draw a horizontal line at the value of My; it will intersect with the moment diagram at the point located at Lh/2 from point A, and the same value for the Lh/2 to the right of point B.
The vertical distance between Mp and the horizontal line is Mp-My. We will estimate tan α to create an expression for Lh: tan α=(L/2)/Mp. The same tan α= (Lh/2)/ /(Mp-My). We adjust to get the final expression for Lh.

Equate L/2/Mp=Lh/2/(Mp-My), Lh=L*(Mp-My)/Mp=(1-My/Mp)*L, for a rectangular section My=Fy*Sx, while Mp=Fy*Zx, dividing My/Mp it will be=Sx/Zx, I corrected the writing, Sx=b*h^2/6, Zx=b*h^2/4. My/Mp=1/1.50. Lh=(1-(1/1.50))*L=L/3.
The horizontal length of the hinge =L/3 for a rectangular-section beam.
The following slide shows the values of My and Mp.

The virtual work method.
The virtual work method saves time by eliminating the need to estimate bending moment values.
Drawing the two bending moments together, as in the case of the static method, in the case of a fixed-end beam, where we draw the two-moment diagrams for the fixed moment at Mp and the maximum moment Mmax Mp, at the hinge. We equate both to the total applied moment.
For virtual work, we equate external work with internal work. External work P*Δ, which is the product of the load by the deformation Δ at the plastic hinge due to the mechanism of collapse. Due to deformation Δ, an angle α is formed.
which is the product of the load and the deformation Δ at the plastic hinge due to the collapse mechanism. Mp is obtained from deformation Δ, and an angle α is formed.
We can consider that tan α =α since α is a small angle. The external work at the LHS is due to F=Mp* total angle (2*α), where 2*α represents the change in angle. This is similar to the yield line analysis for slabs.

The internal work= 2*Mp*α, where α=Δ/(L/2), P*Δ=2*Mp*2*Δ/L, Mp= Pp*L/4. For the sum of the moments at the hinge, P/2*L/2 = p*L/4 clockwise, which balances with M = P*L/4.
The following slide shows the value of Pp using the static method or the lower-bound method; it is the same as the value estimated earlier.

A practice problem for a simple beam: how to estimate the Collapse load for the beam?
Using the given sections of all of A992 steel and the plastic moment, determine the value of Nominal load Pn for a W18x76 section. The following slide shows how to determine the plastic moment value.

The lower-bound method for evaluating the Nominal load value for the practice problem is shown on the following slide.

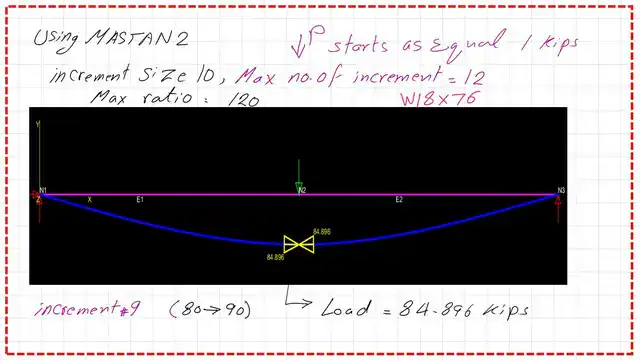
Using the Upper theorem, we equate the product of Pn*Δ by Mn by 2θ. The Pn is equal to 84.895 Kips.

Using Mastan2 to verify the previous result, the P start load of 1 kip has a maximum ratio of 120. The nominal load is found to be equal to 84.895 Kips for the Given W18x76 section, where Fy=50 Ksi
The value of the Plastic Moment is 8150 kips. inch, the next slide image shows the given value.

The PDf file for this post can be viewed or downloaded from the following document.
This is valuable data regarding the structural analysis – III. colincaprani.com
For the next post, Collapse load for indeterminate beam. How to get the collapse load for an indeterminate beam?The beam is fiexd at one end and simply supported at the other end.