Last Updated on October 12, 2024 by Maged kamel

Solved Problem 10-2: How do we Use Table 3-2 For Shear Value? 

A solved problem 10-2, check shear adequacy for the selected section.

This post has two parts. The first part discusses solved problem 10-2, while the second part discusses the nominal shear for steel beams based on CM#15 and specification 2016.

This is a solved problem 10-2 from Prof. Mccormack’s book. There is a beam with a w section W21x55 for which the yield stress Fy equals 50 ksi. Check the adequacy of this beam to the shear using Table 3-2.

Table 1-1 shows all the relevant data for W21x55. A section of W21x55 is drawn, as shown in the small sketch on the left side.

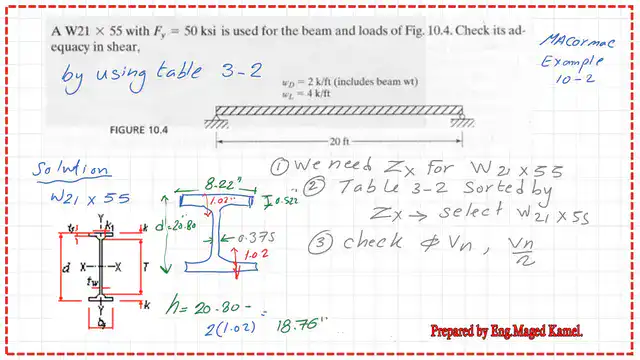
From Table 1-1, we will get the value of the plastic section modulus Zx for the W section W 21×55, which is 126.0 inch3.

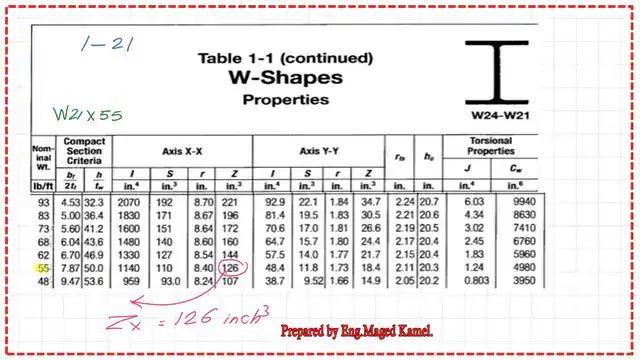
From Table 3-2, where the plastic section modulus Zx is sorted. In the W section W 21 x55, the LRFD value for the nominal shear can be obtained from the final column. The value equals 234.0 kips, which matches the same figure from the previous post.

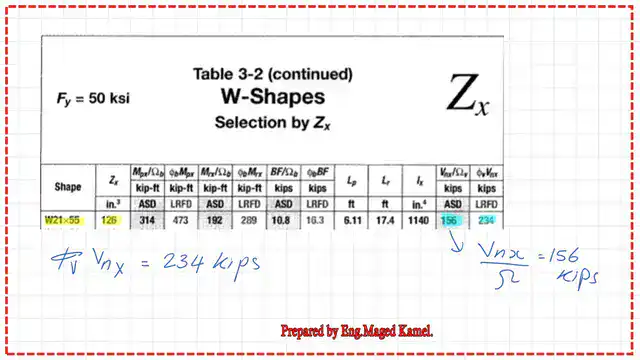
The ASD value for the allowable Nominal shear strength is in Table 3-2. We can find the value for the ASD shear strength, which is 156.0 kips. The attached image shows the figures for both the LRFD and ASD.

AISC specification provision for the design of Members for shear-CM#15.

Chapter G is the designated chapter for the design of members for shear.

Clause G-1 is for the general provisions. Item G2 deals with stiffened and unstiffened steel sections, including W, M, Hp, and S. The other sections not included in G2 are shown in G3, G4, G5, G6, G7, and G8. Please find the data in the next slide image.

The next slide shows the Nominal value for shear.

There is a new term, Cv1. Unlike CM#14, the coefficient of shear was Cv. There is a user note that for all current A6 steel, W, S, and Hp sections, the ratio of h/tw confirms the requirement of 2.24*/sqrt(E/Fy) except W44x230. W40x149 and some other sections do not confirm. We will check section W40x149 ‘s ratio for h/tw. Please check the next slide.

The Kv coefficient equals 5.34 for the unstiffened web. While for stiffened web, Kv equals 5+5/(a/h)^2. The term a is the precise distance between the transverse stiffeners. While h is the clear distance between flanges.

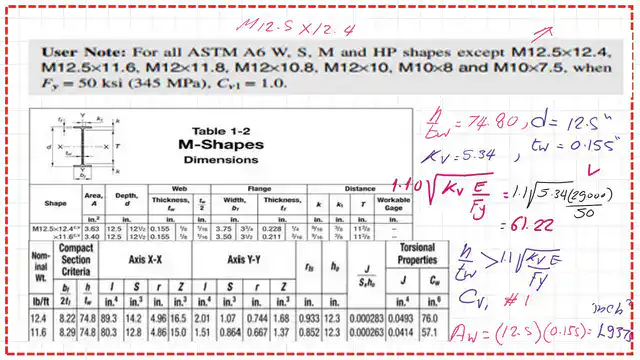
There is a user note for sections. A6, W, S, M, and Hp confirm the requirement of 1.10*/sqrt(KC*E/Fy) except M12.50×12.4. M12.5×11.60, M12x11.80, and some other sections do not confirm. We will check section M12.5×12.40 ‘s ratio for h/tw. Please check the next slide.

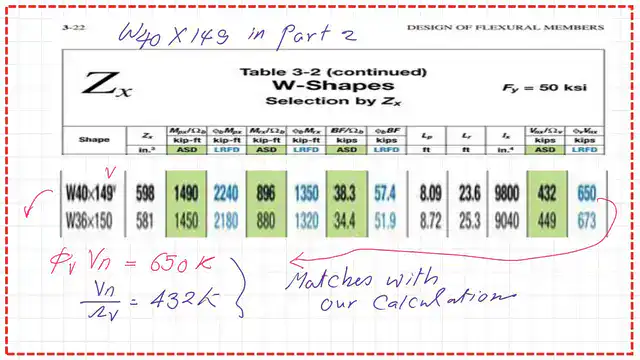
Check section W40x149 for shear and estimate the Nominal shear strength.

For the W40x149 section, there is a list of the data, area, flange width and its thickness, web thickness, and h/tw. The ratio h/tw equals 54.30; when we compare with 2.24*sqrt*(E/Fy), which equals 53.94 for Fy=50 ksi, we find that h/tw for W40x149 is bigger than 53.94 but smaller than the 1.10*sqrt(Kv*E/FY) which equals 61.22 for Fy=50 ksi. Cv1 value equals 1.

The factored nominal shear for section W40x149.

The next slide provides a detailed estimate of the strength of the LRFD design of the shear and the ASD design for the shear.PHi*Vn equals almost 650 kips, and the Vn/lambda=432 kips; please refer to the next slide for more details.

We use Table 3-2 to check the estimated factored shear load; we will find a match between the previously estimated values and those from Table 3-2, as we can see from the next slide.

Check section M12.5×12.40 for shear and estimate the Nominal shear strength.

To check the M12.50×12.4 section, which is included in the user note, we find the h/tw ratio from tables 1-2 for M sections; it equals 74.80. The depth is 12.50″, and the tw=0.155″. The h/tw is more than 1.1*/sqrt(Kc*E/Fy), which equals 31.22 for Fy=50 ksi; please refer to the next slide image for more details.

I use the graph between Vn and the ratio h/tw for M12.5×12.4, represented by point 3 on the x-axis. To find Vn, it equals Cv1* (0.6*)* Aw. We estimate Cv1, which is 0.818, less than 1. Aw=d*tw, and Fy equals 50 ksi. Vn=47.55 kips.

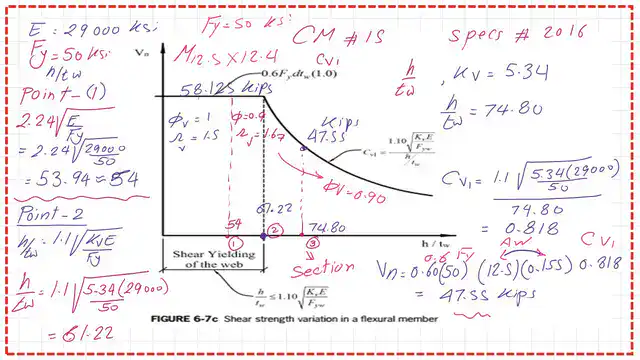
We have reached the end of our post, which is the factor shear stresses for M12.50×12.4. Please refer to the next slide image for more details. Phi is equal to 0.90, and omega is equal to 1.67. Thanks a lot.

A good resource for the shear stress limit state.

The previously solved problem was checked using the AISC provision in this post.

For a solved problem for the S steel shape for shear, please refer to post-41s-Nominal shear strength for S41x121.

This is the next post, post 24: Deflection of steel beams.