Last Updated on March 21, 2024 by Maged kamel

Solved problem 13-28 from Prof.Iqbal’s book.

This is the content of the lecture, how to use table 4-1 from NCEES Reference Handbook 9.5.

We are going to have a look for a solved problem from Prof. Iqbal’s book and the main title is how to use table AISC table 4-1 from the table, we can estimate The Φ*Pn stress. hence we can work on LRFD  and ASD.
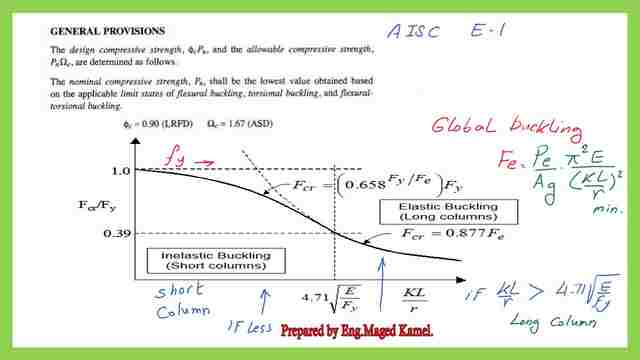
The Euler buckling of Pcr=pi^2 EI/ (k*L)^2. The famous 6 cases, for the k value of columns and the recommended values as a correction. for part of these cases.

This curve we have already discussed, at the value for KL/r = 4.71* sqrt of (E/Fy) is the parameter that distinguishes between short columns and long columns. if the value of KL/r > 4.71* sqrt of (E/Fy), then the column is considered as a Long column, and hence the Euler Elastic stress. The division of pi^2 EI/ (kl)^2 over the area then the stress will be (pi^2 E/ (kl/r)^2).

This is a table quoted from FE Reference handbook in which there is a list of W sections, for which the area, depth, flange width& thickness, and inertias about axis x and axis y are given.

The Fcr for the long column will be considered elastic. stress the value then can be multiplied by the area.

Detailed illustration for the Solved problem13-28 from Prof. Iqbal’s handbook.

A solved problem is from M.Iqbal, A w12 x50 is used as a column as shown, Fy=50 ksi, the support is fixed at the bottom, and with a guide roller at the top, it is required to estimate the available strength in axial compression in kips,  select the correct answer from the following options 1) 90 kips, 2)270 kips 3)360 kips 4)660 kips.

For the solution,   the roller allows movement delta, but the slope is zero. and provide a moment. As if fixed from the top, it contains both movement and Fixation

, the elastic curve is as shown, the tangent here is the angle which is zero, and the slope at the bottom is also zero.

Step-1 -What is the data for W 12x 50 from table 1-1? inch 2, the Ix =391 inch4, the r x is 5.18 inch2 and the ry= 1.96 inch 2 for both directions, the K value is the same =1.2 as recommended for solved problem 13-28.

So we will convert, always the tables deal with K*L/ry, if I have KL/r in the x-direction, we will make k fake x by dividing Kx/(rx/ry), so to enable comparison between values in the x and y- direction, and to use the table as well.

The K fake in x-direction will be 1.2/ (rx/ry), so in this solved problem, our rx = 5.18 and ry is = 1.96, so the value will be =1.2/(5.18/1.96)=0.4, then will be multiplied by Lx=15 feet. the product is 6 feet, to be compared with Ky *Ly .

We check with the larger value The calculation for Fe, will be estimated after comparing, K-fake lx which is  6 feet with the Ky ly, which is 1.2*15=18 feet, which is the bigger, so buckling is governed by the weak axis, then we estimate Ky*ly/ry= 1.2 x15 x12/1.96=110.2, to know whether this column is short or long.

We estimate 4.71sqrt of (E/Fy), and the value is 4.71sqrt(29×1000/50)=113.43 > Ky*ly/ry. This column is a Short column.

Fe can be calculated as Fe=Pi^2E/ (kyly/ry)^2, We will get 23.586 ksi, then for Fcr equation 0.658 ^(Fy/Fe)*fy, the power is (50/23.5867)*50.

The Fe will be= 20.59 ksi,  Pn =Fe multiplied by the area, then the  Φ*Pn will be equal to 0.9 x(20.59)*(14.6)= 270.55 kips.

This is the final answer for solved problem 13-28. But there is a table that can estimate the same value for Solved Problem 13-28. This table is 4-1, which is based on Fy= 50 ksi , the w section is placed as w14, w12,w10.

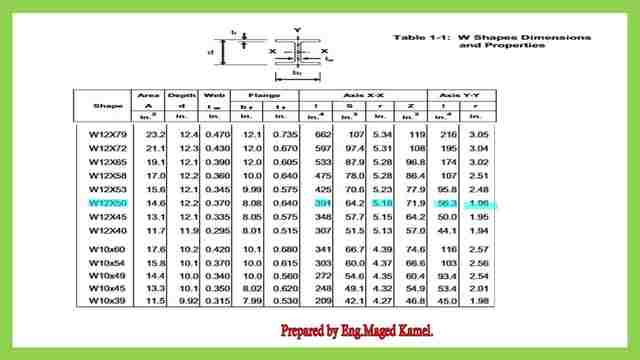
In our Solved Problem 13-28 section is W12x50 will be first located, then as a vertical column and checked with the intersection of the Ky*ly in Feet, which in our case is 18 feet.

This is the pdf file used in the illustration of this post.

This is the next post Two Solved Problems for column analysis.
For a valuable external resource, Concentrically Loaded Compression Members.