Last Updated on September 7, 2024 by Maged kamel

How do we analyze steel beams? Solved problems.

The difference between analysis and design of steel beam.

The difference between analysis and design problems is that for the analysis, the section is given, and a check of stress is needed, while for the design, the loads are provided, and it is required to find the section.

Analysis of steel beam at zone-1.

The solved example is 5-3 from Prof. Segui’s handbook. The beam shown in Figure 5.11 is W16x31 of A992 steel, for which 16″is the overall height or nominal depth, while 31 is the weight in lbs per linear ft of A992 steel, where Fy=50 ksi. It supports a reinforced concrete floor slab that provides continuous lateral support of the compression flange. 
Here, the compression flange is mentioned as being supported continuously, which means we are dealing with a plastic range or zone -1.

Our lambda λ between 0 and λp, and Mn=Mp=Fy*Zx.

The beam shown in Figure 5.11 is W16x31 of A992 steel. W16x31, 16″ is the overall height, while 31 is the weight in lbs per linear ft of A992 steel, where Fy=50 ksi.

How do we estimate the Ultimate load and Ultimate Moment?

The weight of the beam, which equals 31 lb/ft, is added to the given uniform dead load; The ultimate load equals 1.2*Wd+1.6*wl=1.2*(0.45+0.031)+1.6*(0.55)=1.4572 k/Ft. We estimate the ultimate moment as equal to Wu*L^2/8.The span length equals 30 feet. The final value of the Ultimate moment equals 164 Ft.kips.Please refer to the Next slide image.

How to check the compactness of the flange and the web of a beam?

We use Table 1 as the first step in analyzing the steel beam. For W16x31 A=9.13 inch2, the overall depth=15.90 inch, the web thickness =0.275 inches, bf =5.53 inch.
The thickness of the t flange is 7/16 inches.

The controlling factor is 3.76*sqrt(E/Fy) for the web=90.55. The λF, which is 6.28   for the flange, is<λp, which is 9.15, then the section will be in the compact zone for the flange, while λw, which is  51.60, is also <90.55. The section will be in the compact zone for the web, the first zone.

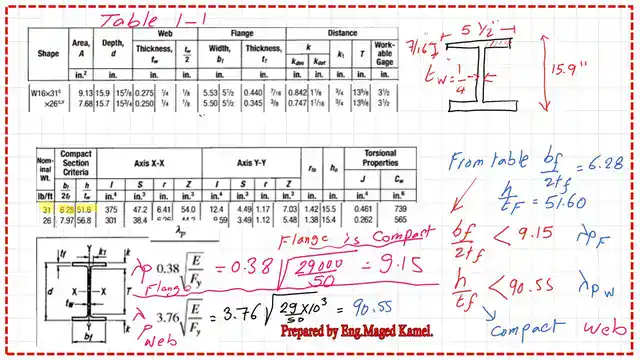
The first step of the steel beam analysis is to get the nominal moment value Mn=Mp=Fy*Zx. From table 1-1, we can get the Zx value, Zx=54.0 inch3.
To get the  Mn=Mp=50*54=2700 inch kips. To convert into ft. kips, we will divide by 12.

LRFD Design-Beam Moment capacity.

Mp=225.0 kips ft. For the LRFD, Our phi is Φb=0.90, then Φb*Mn=0.90*225.0=202.50 ft. Kips.
The Ultimate moment, acting on the section, should be <= Φb*Mn.

As estimated earlier, the section can carry 202.50 Ft.kips. This section is adequate for analyzing the steel beam for the LRFD design. This is the end of the analysis of the steel beam.

ASD design.

While for the ASD Design, Wd= uniform load+own weight=450+31, Wd=481 lb/ft, and WL=550 lb/ft, adding together for Wt, the Mt=(480+550)*30^2/8/1000=116.0 ft. kips.

This is the total Moment. For Mn =225.0 ft. kips, divide by the omega Ωb, 1.67. M all =225/1.67=1350.0 ft.kips. The section can carry 135.0 ft. kips and is only subjected to 116.0 ft. kips; the section is safe.

This section is adequate for analyzing steel beams for the ASD design. The idea of the example is that the section of the beam carries a slab with studs to provide the continuous bracing, then a section was selected Bf/2tf, lambda λF was< lambda λp flange also, λw is<λp for the web.

A second problem is to check the compactness of a given section.

This is an example from Lindeburg. Establish whether a W21x55  beam of A992 steel is compact or non-compact. An analysis of steel beams is required.
There are four options. First is the A992 steel,  with Fy=50 ksi.
For W21x55, the overall depth is 20.80″, which is highlighted. The web has a Thickness of 3/8″ or 0.375″ t-web. I draw the section, Bf=8.22″, and its thickness =0.522″.
To estimate the controlling lambda, first, we need to find the value of Tf/2Tf for flange, which is 8.22/2*0.22=7.87, λp for flange =64.70/sqrt(50)=9.15. Then, λf<λp for the flange.

For the second part, we will correct the web thickness as 0.375″, h, as estimate =(20.80-2*0.522)/0.375, where tweb=0.375. If we divide 20.80-2*0.522 by the calculator, we get hw, hw=19.756″/0.375 = 52.68.

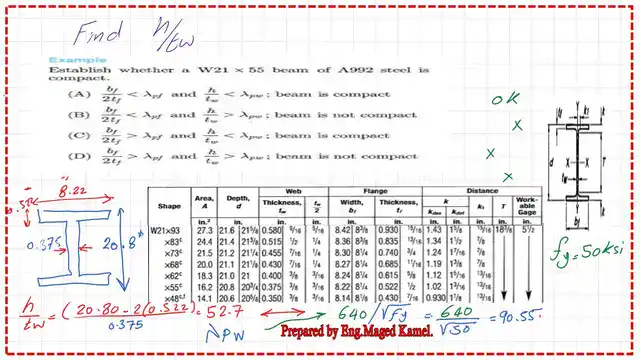
Check against λp, which is  640/sqrt(50)=90.55, then 52.55 is <90.55; since bf/2tf< λp f and hw/tw is< λp t, then option A is correct. This is the end of the analysis of the steel beam. Option A is the proper selection.

For bending members, please refer to this link from Prof  T. Bart Quimby, P.E., Ph.D. F.ASCE site.

For the next post, A Solved problem-4-7-1, how to design a steel beam.