Last Updated on January 4, 2024 by Maged kamel
- A solved problem for x-y-z values by LU decomposition for a 3×3 matrix.
- Step-2-Derive the expression for U2 and L2 matrices.
- Step-3-Derive the expression for the inverse matrix L-1 matrix for the solved problem for x-y-z.
- Step-5-Get the value of C- matrix.
- Step-6-Get the value of the X- matrix for the solved problem for x-y-z.
- The last values for x,y, and z are for the solved problem for x-y-z.
A solved problem for x-y-z values by LU decomposition for a 3×3 matrix.
We have three simultaneous linear equations, it is required to get x,y, and z for these equations by using Lu decomposition.
We start by converting matrix A into U1 matrix by letting a21,a31 values are zero to constitute an upper matrix.
Reverse the signs of the estimated two factors to get the value of L21 as=(+4) and for L31 as=(+2). the l32 is unknown.
For the a33 since it is already 0, we need not create any multiplication. This zero will be placed as the l33 value in our created L1 lower matrix.

The factors shown are (-a21/a11) and (-a11/a31). The first factor value=-(8/2)=-4, while the second factor=(-4/2)=-2.
The U1 matrix is formed for the first row (2 1 4) which are the values of u11,u12, and u13.
For the second row of the U1-matrix( 0 -7-14) which are the values for U21, U22 U23, the last row is(0 9 -9).
Step-2-Derive the expression for U2 and L2 matrices.
Convert a32 which is (9) to zero by multiplying by (-9/-7)R2 adds the value to R3, and we have used -7 as a second pivot, and the result which is (+9/7)-7+9=0 will be the value of u32, the corresponding L32 value is the reversed sign factor which is(-)*(9/7)=-9/7. The detailed calculations are shown in the next slide image.

The final shape of U2 and l2 will constitute the L and U matrices both of these matrices are 3×3 matrices, hence A can be set to be the product (L*U). A routine check of the product of L*u will produce the same elements of matrix A to be performed.
Step-3-Derive the expression for the inverse matrix L-1 matrix for the solved problem for x-y-z.
We will use the augmented matrix to get the inverse matrix L-1 value which will be (3×3 matrix). The process will continue till the left side of the matrix is an identity matrix and the right side of the augmented matrix will be the required inverse matrix of the lower matrix, denoted as Ll-1.
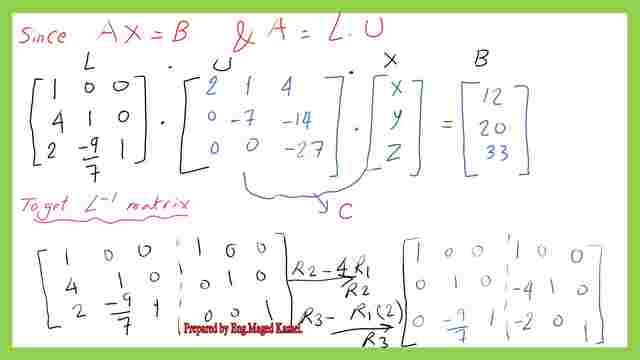
Step-5-Get the value of C- matrix.
The C matrix is set to the multiplication of the lower matrix inverse by the matrix, B, and expressed as =L-1*B, both matrix’s values are known.
The C matrix is a (3×1). The detailed calculations of the multiplication of the rows by columns are shown in the next slide images.
We have U*x=C. We can write the matrix of U and the matrix of X and equate that multiplication to the matrix C.

Step-6-Get the value of the X- matrix for the solved problem for x-y-z.
C-matrix is =(12 -28 -27) it is 3×1 matrix. We have U*X=C, and the inverse matrix U-1 is needed to be estimated to get the expression for x=U-1*C. So we can estimate the final values of x,y, and z, by multiplying by the inverse matrix of U which is (U-1)
We will derive the expression for the inverse matrix -U-1, by using the augmented matrix method. The full details of the necessary calculations are shown in the next two slide images.

The steps followed to get the inverse of the U matrix can be checked from the next slide image.

The inverse of U is also an upper matrix and is called U-1 and written as ( 1/2 1/14 1/27) for the first row, ( 0 -1/7 12/27) for the second row, and ( 0 0 -1/27) for the third row. The inverse of the Upper matrix is to be multiplied by the matrix C, to get the values of x,y,z.

The last values for x,y, and z are for the solved problem for x-y-z.
The multiplication of the inverse of matrix u by matrix c is shown and the final values for x,y, and z can be found to be=(3,2,1). The routine check for the estimated values for x,y, and z will be performed to satisfy the given three equations. The calculations are shown in the last slide image.

We substitute the three equations with the values of x,y, and z and check whether these values satisfy the equations or not.

This is the pdf file used for the illustration of this post.
The next post: Solved problem 9-5 LU decomposition.
This is the Omni calculator for estimating various items of linear algebra -LU Decomposition Calculator.
This is a link to another –Calculator for matrices.

