Last Updated on September 1, 2024 by Maged kamel

Types of frequencies of compounding.

The compounding frequency is the number of times per year (or rarely, another unit of time) the accumulated interest is paid out or capitalized (credited to the account), regularly.

The frequency could be yearly, half-yearly, quarterly, monthly, weekly, daily, or continuously (or not at all, until maturity). Quoted from the definition of compound interest.

The balance of $1 for the interest of 100%-compounded semi-annual.

This is the first type of compounding semi-annually. From the last post, we have estimated the future value of $1 compounded yearly.

After one year based on compound interest, 100% compounded yearly. The value was $2.00, we want to find the balance value based on 100% compounded-semi annually. The first step is to get the future value at time t1=0.50 year=1 semi-annual. We can see from the graph the Fv-1=(1+2)*0.50=$1.50.

For the value of FV-2 after one year. We get the multiplication factor for the value at t=2 semi-annual, which is=(1.50)*1.50)/1.00=$2.25.

The compounding starts after the first semi-annual and the slope gets increased based on the new ratio. This is the process of changing from linear to exponential function at t=0.50 year.

Recall that the Fv equation=P0*(1+i)^n. In this case p0=$1, new i/n=(100/100)/2=50%. the power raised is (i*t)=2*1=2.00. The future value obtained matches the value in Table 4.13. the FV-2=(1.5*1.5)/1=$2.25.

The balance of $1 for the interest of 100%-compounded-quarterly.

This is the second type of compounding-Quarterly.

From the last post, we have estimated the future value of $1, after one year based on a compound interest of 100% compounded yearly. The value was $2.00, we want to find the balance value based on 100% compounded-quarterly.

For the value of FV-2 after one year. We get the multiplication factor for the value at t=1 quarter of a year, which is=1.25.

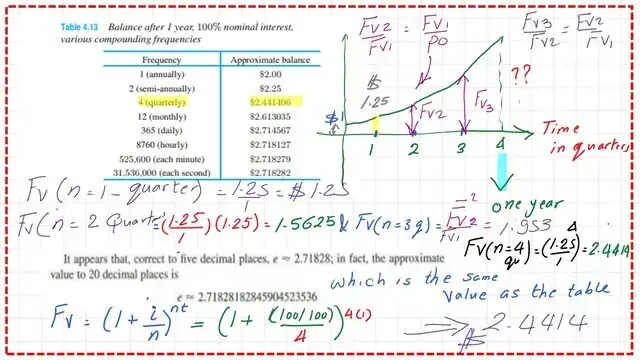
The slope gets increased based on the new ratio. This is the process of changing from linear to exponential function at t=0.25 years.

Recall that the Fv equation=P0*(1+i)^n. In this case P₀=$1, new i/n=(100/100)/4=25%. The power raised is (i*t)=4*1=4. The value obtained matches the value in Table 4.13. the FV-2=(1.25*1.25)/2=$2.4414.

The balance of $1 for the interest of 100%-compounded-monthly.

This is the third type of compounding monthly. From the last post, we have estimated the future value of $1, after one year based on a compound interest of 100% compounded yearly. The value was $2.00, we want to find the balance value based on 100% compounded monthly.

For the value of FV-2 after one year. We get the multiplication factor for the value at t=1 month of a year, which is=1.083333.

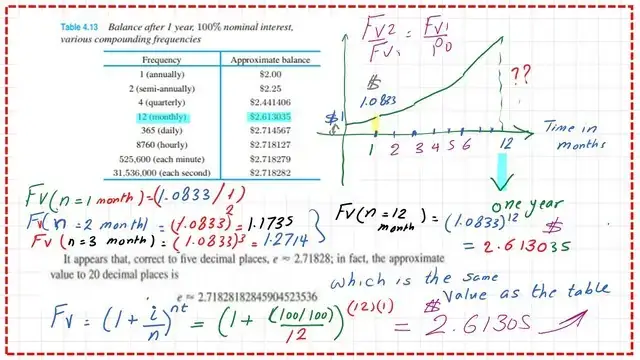
The compounding starts after the first month and the slope gets increased based on the new ratio. This is the process of changing from linear to exponential function at t=(1/12) year.

Recall that the Fv equation=P₀*(1+i)^n. In this case P₀=$1, new i/n=(100/100)/12=8.3333%. The power raised is (i*t)=12*1=12. The value obtained matches the value in Table 4.13. the FV-2=(1.08333*1.08833)/1=$2.4414

The balance of $1 for the interest of 100%-compounded-daily.

This is the fourth type of frequency which is compounded-daily. From the last post, we have estimated the future value of $1, after one year based on a compound interest of 100% compounded yearly. The value was $2.00, we want to find the balance value based on 100% compounded monthly.

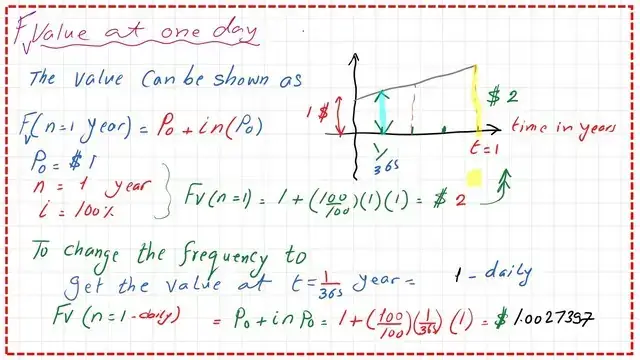
For the value of FV-2 after one year. We get the multiplication factor for the value at t=1 day of a year, which is=1.0027397.

The compounding starts after the first day and the slope gets increased based on the new ratio. This is the process of changing from linear to exponential function at t=(1/365) year.

Recall that the Fv equation=P₀*(1+i)^n. In this case P₀=$1, new i/n=(100/100)/365=2.739726*(10^-3). The power raised is (i*t)=365*1=365.
The value obtained matches the value in Table 4.13. the FV-2=(1.0027397.*1.0027397)/1=$2.714567.

For a given interest of 6%, for interest to be compounded annually, it will be the same value as 6%.
For different frequencies like semi-annually, and quarterly, the interest value will change. the nest slide image shows these values.

When the number of years exceeds one year, it will be raised as power and multiplied by I.

These are some examples of the different interest rates, with different, n values of years.

Solved example 3.7 to estimate the future value of a given deposit.

This is solved Example 3.7, for which it is required to estimate the future value for a given Po=$500, with 6% interest compounded quarterly, for n=3 years.

The following post is post-6b-Introduction to a solved problem for compound interest

For a useful external resource, Engineering Economy. Applying Theory to Practice.