Last Updated on March 31, 2023 by Maged kamel

Area and Cg of a triangle.

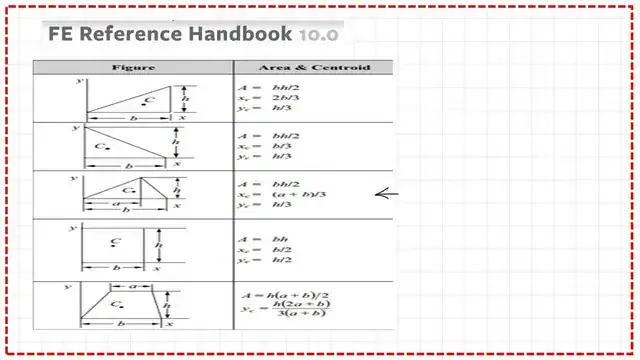
Reference handbook 10.00 values for areas and Cg.

To get the area and Cg for a triangle, we will proceed to divide the triangle into two right-angle triangles, it is required to get the same data as obtained from the FE reference handbook as attached in the next slide image. the case of a triangle is the third case in the table.

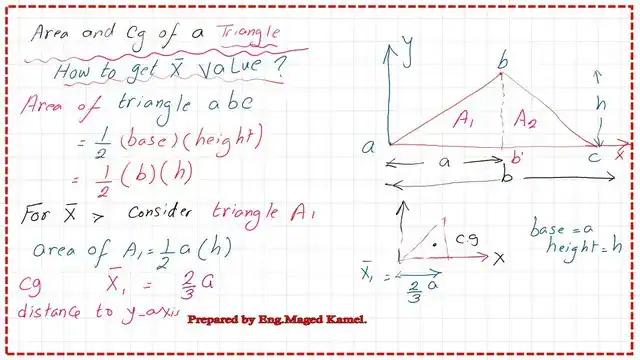
Area and Cg of a triangle-x bar estimation.

We will divide the triangle into two triangles as A1 and A2, the first triangle area can be found as =0.50*base* height, the base length equals a, and the common height of the triangle=h. he Area A₁=0.50*a*h. As for the second triangle.

X bar for a triangle.

The get x bar for the triangle of area A₁, it can be found to be=(2/3)*a from the y-axis passing by point a located at the left side of the triangle.

The second area is A₂, its base=(b-a) and the height=h, so the area A₂=0.50(b-a)*h. While the cg distance for area A2 to the y axis is termed as x bar2 will be =a+(1/3)*(b-a).

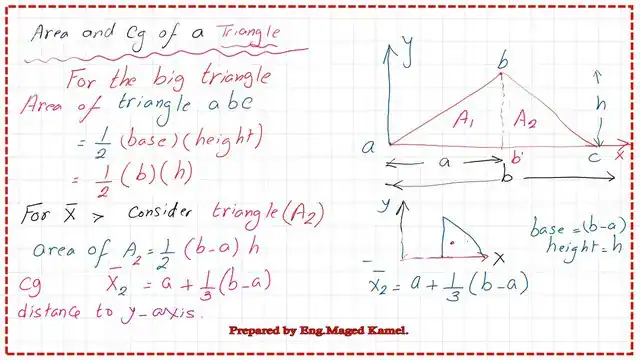
The final value for the X- bar for the triangle can be obtained by summing the product of A*x and equating the value to the product of the total area *x bar of the triangle.

The sum of the product of area1*X1 bar plus the sum of area 2by x bar2 is shown in the previous slide image.

As we can find out that the final first moment of area for the whole triangle equals (h/6*(ab+b^2)) after we have simplified the terms of multiplications.

The final x bar for the triangle or the distance between the Cg of the triangle to the y-axis can be found as equal to (1/3)*(a+b) and matches with the Reference Handbook-10 value of the area and Cg of a triangle.

Area and Cg of a triangle-y bar for a triangle.

To get the value of the triangle y bar for a triangle, we will divide the triangle into two triangles as A1 and A2, and make the necessary calculation to get the y bar for each triangle. The first triangle area can be found as =0.50*base* height, where the base length of the whole triangle =a, while a is the distance from point a to point b’. The common height of the triangle=h.

The Area A₁=0.50*a*h.Y1 bar which is the Cg vertical distance to axis x cab be found to be=h/3. As for the second triangle. The get the y- bar for the triangle of area A₂, it can be found to be=(1/3)*h from the x-axis passing by point a on the left side of the triangle.

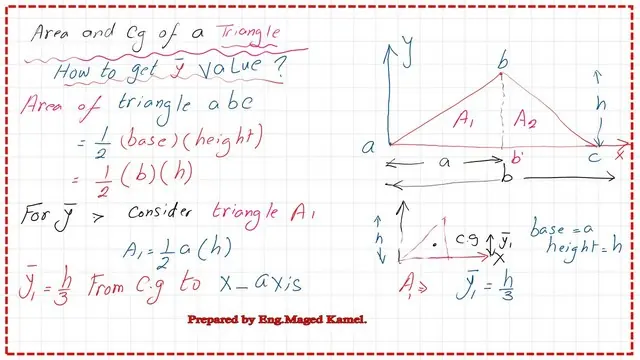
The second area is A₂, its base=(b-a) and height=h. b is the base of the whole triangle ABC. We can divide the product of A2*y2 bar by the area A2. The area A₂=0.50(b-a)*h. while the cg distance to x- axis y- bar-2=h/3.

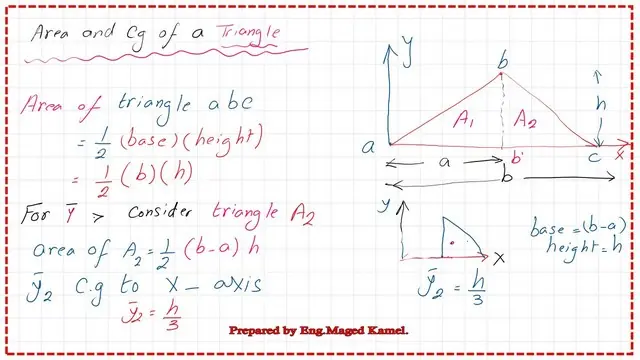
The final value for The Y- bar for the triangle can be obtained by summing the product of A*y for Areas A1 and A2 and equating the value to the product of the total area *y bar of the triangle. As we can find out that this product of (A1y1 bar+A2y2 bar)=b*h^2/6.

Y bar for a triangle.

The final y bar or the distance between the Cg of the triangle to the x-axis can be found as=h/3. This value matches with the Reference Handbook-10 value of the area and Cg of a triangle.

This is a link for the pdf file used in the illustration of this post.

For a good external reference, please refer to the Centroid of an Area by Integration.

This is the link of the next post will be Area and Cg for a rectangle.