Last Updated on December 19, 2024 by Maged kamel

Mohr’s Circle of inertia.

In this post, we will be starting our discussion about Mohr’s circle of inertia. Still, we will use the relation of x’ and y’ for an area about an inclined axis, with the x and y distance for the same area but about horizontal and vertical axes x, and y. The Inertia Ix is bigger than Iy and Ixy is positive.

.

Introduction to Mohr’s circle of inertia.

Brief content of the post.

The post items that will be explained are summarized here.

When Ix is greater than Iy, we will begin to learn how to draw Mohr’s circle of inertia using the provided data for two points. As we can see, y’=ycos θ -x sin θ represents the perpendicular distances from the little area dA to x’ and the axes. In contrast, x’=xcos θ + y sin θ.

We have two theories regarding the composition of Mohr’s circle of inertia: is it a shifted circle or a centric circle with the intersection of Ix, Iy, and Ixy as its center point?

What is the value and direction of the primary angle 2θp at the third point?

What are the values of Iu and Iv, or the maximum and minimum moments of inertia, along with their directions, constitute the fourth point?

Where is the pole point in Mohr’s circle and the normal view is the fifth point?

How do you draw Mohr’s circle of inertia?

Firstly, how can Mohr’s circle of inertia be drawn when the Ix value exceeds the Iy value?

We begin by locating point X, which has the coordinates Ix, and Ixy as positive values. Point Y, on the other hand, has the coordinates (Iy,-Ixy). A circle’s center is where the intersection of these two locations with the vertically shifted axis occurs.

This circle’s radius is equal to the square root of Ixy^2+The difference between (Ix-Iy/2)^2. The axis that connects point X to the circle’s center is known as the X-axis.

On the other hand, the Y-axis is the axis that connects point Y to the circle’s center. Our axis, X’, is produced by connecting the point x’, which has the coordinates (Ix’, Ix’y’), to the center of Mohr’s circle of inertia. Point y’, which has a coordinate of (Iy’,- Ix’y’), is the opposite point.

The enclosed angle of 2θ, which is twice the value of theta from the normal view—from which we derived the three equations Ix’, Iy’, and Ix’y’—between axis X and axis x’.

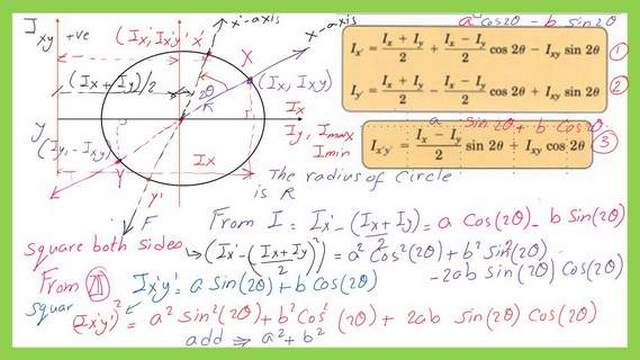
Given that Mohr’s circle of inertia has both points X and X’, it follows that the square of the values of (Ix’-(Ix-Iy)/2) and the square of the value of Ix’y’ can likewise be used to determine the radius of that circle.

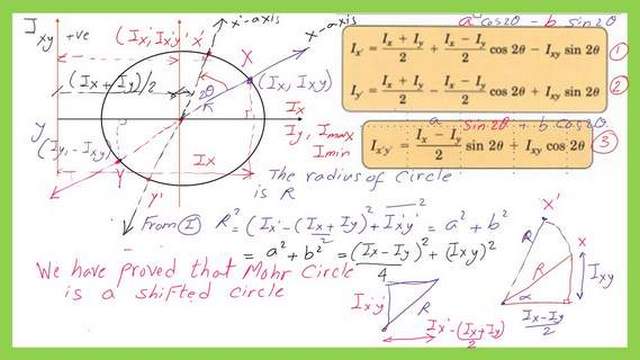
How to prove that Mohr’s circle of inertia is a shifted circle?

As seen in the slide, we have three equations for Ix’, Iy, and Ix’y’ from the previous post.

Two points on Mohr’s circle of inertia—a shifted circle with the values of the moment of inertia, Ix, and Iy—are represented by the three equations.

The sum of the squares of (Ix’-(Ix+Iy)/2 and Ix’y’ should equal the sum of the squares of (Ix-Iy)/2 and Ixy to demonstrate that the Mohr circle has been relocated.

The term an in equation 1 can be used to equal (Ix-Iy)/2, while the term b can be used to equal Ixy if we subtract the value of (Ix+Iy)/2 from both sides. Acos(2θ)-bsin(2θ) equals Ix’-1/2(Ix-Iy). Its value for Ix’y will be (a* sin(2θ)+b*sin(2θ).

Square (Ix’-1/2*(Ix+Iy) will give a^2*cos^2(2θ)+b^2 sin^2((2θ)-2a*b*sin((2θ)*cos((2θ).

While squaring Ix’y’ will give a^2*sin^2(2θ)+b^2 cos^2((2θ)+2a*b*sin(2θ)*cos(2θ).

If we have a look at the fourth slide. Adding together will give (a^2+b^2), which we will rewrite as (Ix-Iy)^2/4+Ixy^2.

This value represents the square value of the radius the square of the distance of Mohr’s circle of inertia and point X.

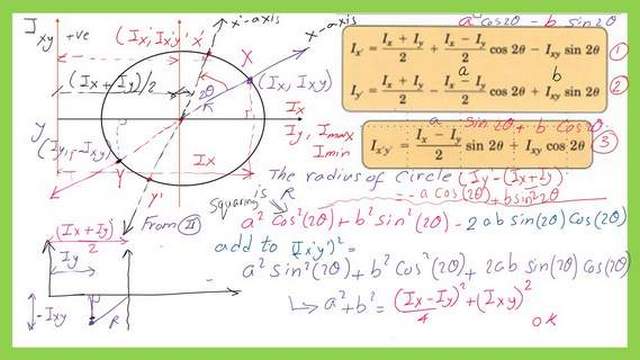
We’ll proceed to the following slide to see what the square of (Iy’ minus (Ix+Iy)/2 plus the square of Ixy will equal. We will move on to equation II and subtract the value of (Ix+Iy)/2 from both sides using the same terms, a and b.

The formula for the new right-hand side is (-a *cos(2 θ) +b sin(2θ).

Adding together the square (Iy’ minus (Ix+Iy)/2 plus the square of Ix’y’ will give (a^2+b^2), which we will rewrite as (Ix-Iy)^2/4+Ixy^2. The result matches with radius value from point X and the center of the circle.

How to find the point of maximum value for inertia?

The point Z, where the Ixy value equals zero, is the greatest value of inertia.

What about the primary axis’s direction? By utilizing an enclosed angle of 2θp in a clockwise direction from the x-axis, one can determine the direction from Mohr’s circle of inertia. In contrast, it has an angle of θp from the x-axis in a clockwise direction when viewed normally.

By utilizing an enclosed angle of 2θp in a clockwise direction from the x-axis, one can determine the direction from Mohr’s circle of inertia. In contrast, it has an angle of θp from the x-axis in a clockwise direction when viewed normally.

The expression of Imax using Mohr’s circle.

One can estimate the value of Imax or Iu by taking the shift, that is equal to (Ix+Iy)/2 plus the radius value. We can draw an angle and obtain the radius value in terms of Ixy, Ix, and Iy by checking the tan 2θp equation.

Thanks a lot and peace be upon you all.

The next post will be an Easy introduction to Mohr’s Circle of Inertia part 2.

This is a link to a useful external resource. Calculator for Cross Section, Mass, Axial and Polar Area Moment of Inertia, and Section Modulus.