Last Updated on March 22, 2025 by Maged kamel
Matrix Operations-part-2.
In this new post, I will introduce matrix operations—part 2, which includes the powers of a matrix. Please refer to the next slide image.
The data are quoted from Prof. Kuldeep Singh’s handbook, which discusses the properties of addition through a solved problem.
Powers of a matrix.
The following property of the matrix operations part 2 is the powers of the matrix. For instance, matrix A with dimension (2×2) consists of 4 elements (1 2, 0 1).
A raise to the power of 2 or A^2 can be done by multiplying matrix A by itself.
If matrix A has a dimension of (2×2), the final matrix will also have a dimension of (2×2).
Let us perform the multiplication. It is easy to consider the first row as a vertical column and multiply it by the first column of matrix A. For (Ab)11, we have (1*1+2*0)=1+0=1. I use the letter B as an indication of the second matrix.
For (Ab)12, we multiply the first row, and after placing it as a vertical column by the second column of Matrix A, we have (1*2+2*-1)=2+(-2)=0.
For (Ab)21, we multiply the second row, and after placing it as a vertical column by the first column of Matrix A, we have (0*2+-1*0)=0+0=0.
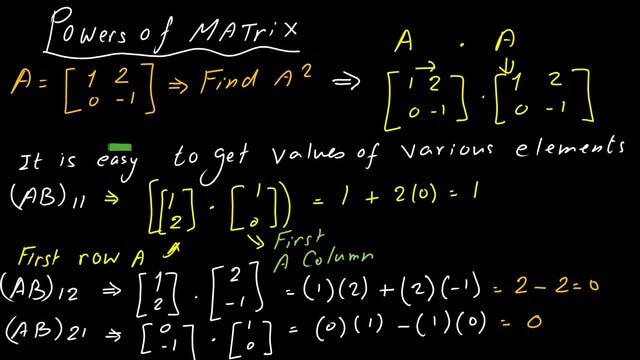
For (Ab)22, we multiply the second row, and after placing it as a vertical column by the second column of Matrix A, we have (0*2+-1*-1)=0+1=1. We can not square each element of matrix A and consider the resulting matrix as A^2.
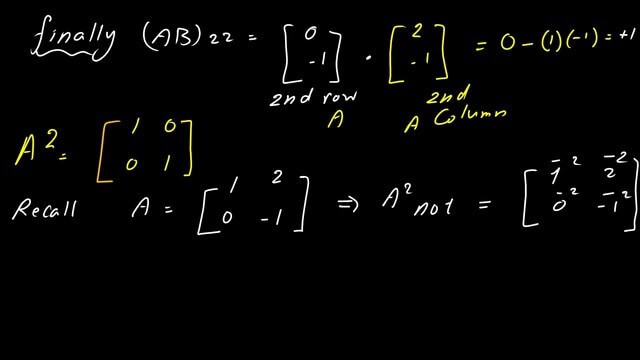
Multiplication of 3×3 matrices.
For the matrix operations-part-2 of multiplying two matrices AxB, matrix A has a dimension of 3×3, while the second matrix B has a dimension of 3×4. Since both matrices have a standard dimension of 3 for the columns of A and the row of b, the final dimension of the product of A by b will be of the dimension of (3×4).
Elements AB11, AB12.
Consider the first row as a vertical column and multiply it by the first column of matrix B. For (AB)11, we have (3*2+5*5+-1*9)=22.
For (AB)12, we multiply the first row, and after placing it as a vertical column by the second column of Matrix B, we have (3*-2+5*0+1*-4)=-2.
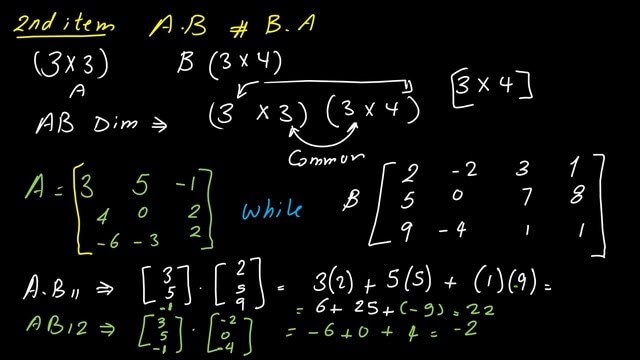
Elements AB13, AB14.
For (AB)13, we multiply the first row, and after placing it as a vertical column by the third column of Matrix B, we have (3*3+5*7+(-1*1)=43.
.For (AB)14, we multiply the first row, and after placing it as a vertical column by the fourth column of Matrix B, we have (3*1+5*8+(-1*1)=42.
Now, we can write down the first row for the product of matrix A by matrix B.
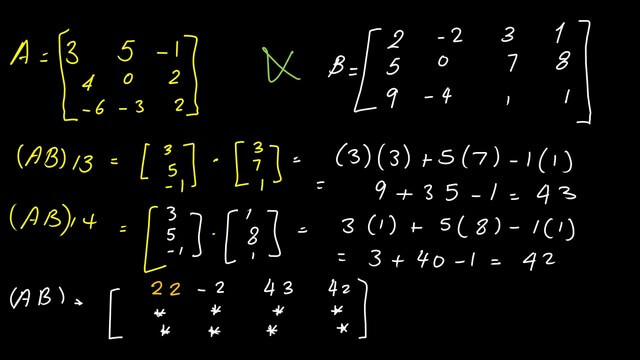
Elements AB21, AB22& AB23.
For (AB)21, we multiply the second row, and after placing it as a vertical column by the first column of Matrix B, we have (4*2+0*5+2*9)=8+18=26.
For (AB)22, we multiply the second row, and after placing it as a vertical column by the second column of Matrix B, we have (4*-2+0*0+2*-4)=-8-8=-16.
For (AB)23, we multiply the second row, and after placing it as a vertical column by the third column of Matrix B, we have (4*3+0*7+2*1)=12+2=14.
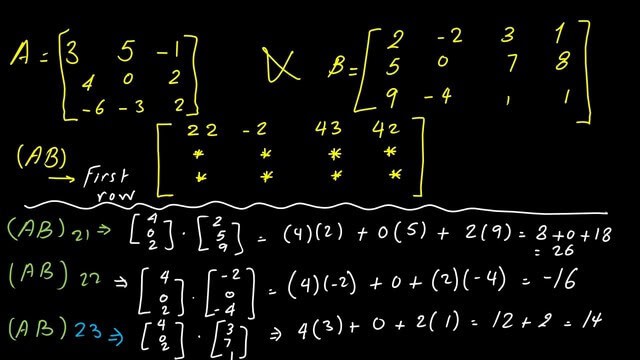
Element AB24.
For (AB)24, we multiply the second row, and after placing it as a vertical column by the fourth column of Matrix B, we have (4*1+0*8+2*1)=6.
Now, we can write down the first & second rows for the product of matrix A by matrix B.
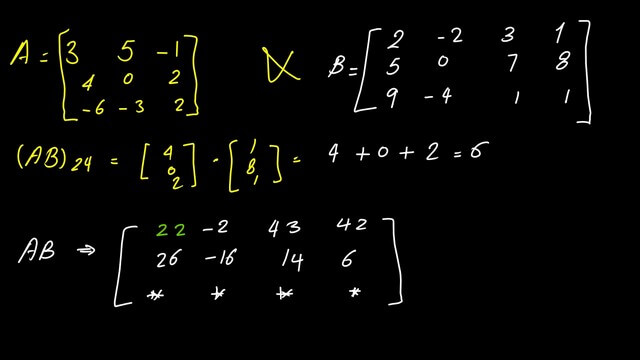
Elements AB31, AB32& AB33 and AB34.
For (AB)31, we multiply the third row, and after placing it as a vertical column by the first column of Matrix B, we have (-6*2+-3*5+2*9)=-12-15+18=-9.
For (AB)32, we multiply the third row, and after placing it as a vertical column by the second column of Matrix B, we have (-6*-2+-3*0+2*-4)=+12-0-8=4.
For (AB)33, we multiply the third row, and after placing it as a vertical column by the third column of Matrix B, we have (-6*3+-3*7+2*1)=-18-21+2=-37.
For (AB)34, we multiply the third row, and after placing it as a vertical column by the fourth column of Matrix B, we have (-6*1+-3*8+2*1)=-6-24+2=-28.
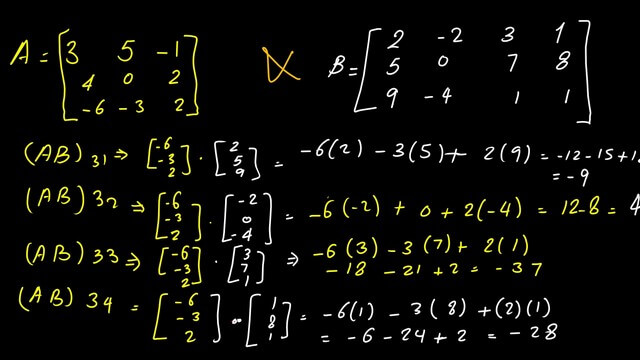
The Product of A by B is shown in the next slide image. We cannot perform the product of B By A since the number of columns in Matrix B is four while the number of rows in Matrix A is only 3. An online matrix calculator verifies the product of matrix A by matrix B.

This is the next post- Solved problem for matrix operations.
For a useful external link, math is fun for the matrix part.
