3a- Elastic and plastic section moduli for a Rectangle.

Last Updated on September 13, 2026 by Maged kamel

Elastic And Plastic Section Moduli.

This video covers two posts: 3a and 3b. The part of the video that covers this post runs from 00:00 to 10:42.

Timestamps for the video.

• 00:00 Elastic section Modulus Sx definition.
• 02:59 Plastic section modulus Zx.
• 06:27 What is the shape factor?
• 06:53 Derive an Expression for y-bar for a rectangular section
• 09:15 Effect of symmetry on the elastic neutral axis.
• 10:24 Elastic neutral axis for stem and unequal angle.
• 10:53 Elastic neutral axis for any shape.
• 11:49 Plastic neutral axis for any shape.

First, we consider the elastic section modulus, Sx. When a rectangular section (b*h) is subjected to a Moment, the stress at the upper fiber has reached yield, and the stress at the lower fiber has reached yield.

Due to the bending Moment, the Beam will deflect in this shape. The upper fiber experiences compression, while the lower fiber experiences tension.

If the load acting on a Beam is increased beyond the load that causes the first yield in the upper fiber, the stress Fy propagates from the upper fiber to the lower one, and the section becomes fully yielded. Thus, we obtain the plastic neutral axis.

The stress profile has changed from triangular to trapezoidal. Ultimately, it becomes rectangular, as shown in the sketch.

If we consider symmetry, the Area above the Plastic neutral axis is half the total Area, A/2, where A is the total Area of the section. o-cession acts on the upper section.

 This force at the plastic stage, Cp=Fy* Area of a Rectangle (b*h/2), or Fy* Area of a Rectangle (b*h/2), will have a tension force Tp equal to the compression force Cp. For the lower portion below the P.N.A., Cp =Tp =Fy*(b*h/2).

Both forces will act on the Cgs, the center of gravity, at h/4 above and below the neutral axis. Theyct is the distance between the tension and compressive forces, and it equals (h/4)+(h/4)=h/2.

 Let us write the following information in an equation, where Cp=Tp=Fy*A/2, while yct=h/2. he p st Momen   Mp=Fy*(A/2)*(h/2).

A new term, Zx, or the plastic section modulus, will appear. he v ue f Zx=( /2)*(h/2) =(b*h)/2*(h/2)=b*h^2/4 ,or Zx=(A/2)*2 y bar. This is one y-bar distance, measured from the Cg of the upper Area to the P.N.A. This y-bar = (h/4)= h/2.

For a Rectangle, the plastic section modulus is Zx = b*h/4. What is the shape factor? The shape e factor is the ratio Zx/Sx (plastic section modulus/elastic section modulus), which equals 1.50.

Section modulus Sx for a rectangular shape-part 1.

This is a general method for estimating the section modulus of a rectangular section at any axis located Kd from the bottom.

1-First, it is required to get the Y bar for the section by summing the first Moment of areas, considering the datum line is at the bottom. he Pr uct A1y1 + A2y2 = At*y bar; since the total Area is known, we can find y bar.

2- We estimate the Inertia about the neutral axis, which we have just evaluated at a distance y bar from the datum.
3- We estimate the y-max value for a Rectangle as y max=d/2; Sx is simply the division of Inertia Ix/ymax.

How do you evaluate Zx, the plastic section modulus for a Rectangle?

A- To estimate Zx, the plastic section modulus, assume there is an axis that divides the whole section into two equal areas and assume that it is apart by a distance Kd from the datum line.

B- Equate A1 and A2 and get the value of k, which is 1/2 for a rectangle=1/2.
B- The Product of  (At/2 )*(y1+y2) will give us the plastic section modulus, where y1 is the distance from the P.N.A to the CG of Area A1, while y2 is the distance from the P.N.A to the CG of Area A2.

If we move to the next slide, due to symmetry, the y-bar we estimated is the distance from the bottom to the elastic neutral axis, which divides the Rectangle into two equal parts.

The Sx value is equal to Ix /y max, where Ix equals bh^2/12, and y_max equals h/2.

The elastic section Modulus Sx for a Rectangle equals b*d^2/6. For I- andSS-shapess, the elastic neutral axis divides the shape into two equal parts due to symmetry.

For the C shape, the symmetric axis is x-x, and the NSA will pass through the X-axis.

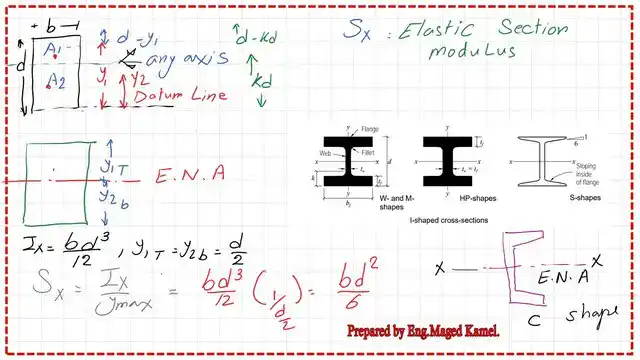
 In the next slide, three shapes are doubly symmetric about the X and Y axes; the EN axes pass through the X-axis.

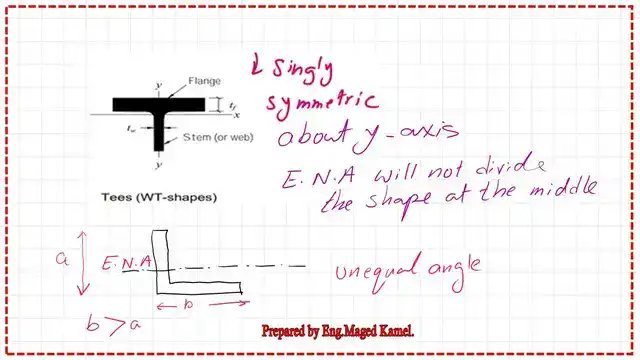
On the next slide, two examples show situations where the E.N. axis does not divide the shape equally. These shapes are a W-shape and an unequal angle.

The elastic neutral axis intersects the stem and is near the upper Flange. For the h second shape, which is an unequal angle, the E.N. axis is close to the lower part of the angle, which contains the longer leg. n angle

The PDF file for this post is available and can be viewed or downloaded from the button below.

Here is the Link to Chapter 8, “Bending Members.” A Beginner’s Guide to the Steel Construction Manual, 14^th ed.

Here is the Link to Chapter 8, “Bending Members.” A Beginner’s Guide to the Steel Construction Manual, 15^th ed.

Here is the Link to Chapter 8, “Bending Members.” A Beginner’s Guide to the Steel Construction Manual, 16^th ed.

The second part of this post will include instructions on estimating the Elastic and Plastic Section Moduli for any section-post 3b.

For a solved problem, please refer to post 4, Solved problem 4-3, for the elastic and plastic sections.