Last Updated on February 25, 2026 by Maged kamel
Solved problem 10-1- Moment Values By Three-Moment Equations For Continuous Beam-3/4.
For our solved problem 10.1, we have completed the selection of the beam section using Plastic analysis and will proceed with an elastic design using the 0.90 rule.

Brief description of the 0.90 rule for the elastic redistribution of the moment.
Utilizing the three-moment equations effectively allows for a better understanding of continuous beams.
Part b of the requirement is to design the beam using elastic analysis with the service loads and the 0.9 rule.
The 0.90 rule is a redistribution method for bending moments that considers 90% of the negative moment. The 10% will be added to the positive moment for an intermediate span.
We add the average 10% value, along with the reduced value between the two supports, to the maximum positive moment at the end span.
For the case of a beam with a continuous edge, the average of 10% of the values is to be added to the maximum positive.
How to use the three-moment equations?
When applying the three-moment equations, it is essential to consider continuity in your calculations.
The three-moment equations for the fixed joint A.
In the method of three-moment equations, at the fixed support, there is an imaginary beam length L0 with a distance equal to zero, so L0=0 at the left side of support A.

From the next slide, review the equation of the three-moment equations. Since there is no moment, we apply the equation of three moments at Joint A, with no elastic reaction at the left span of Joint A.
The second beam has a concentrated load, P1. Its elastic reactions can be estimated after we draw the ding moment diagram; the maximum moment = P1*L1/4.
I will not write the values of P1 or W1 until I obtain the final relation in matrix form, at which point I will substitute these values.
The elastic reaction value is the area of half of the bending moment triangle, which is 0.50 *(P1*L/4)*L1/2=P1*L1^2/16, which is the half value of the triangle.
That was the value of the elastic reaction for the concentrated load.
But, we have a uniform load with intensity W1, which causes a bending moment = W1*L1^2/8. The elastic reaction value is the area of half of the parabola, which is=1/2*(2/3)*L2*(W1*L^2*(1/8)).
This value is the elastic reaction at the right side of joint A. The area of the half of the parabola=1/2*(2/3)*L1*(W1*L1^2/8)= W1*L1^32/24.
To solve the equation by using matrices, consider the following:
1-Put moments MA, MB, MC, and MD as a vertical column matrix (4×1).
2-While the row matrix is (1×4), from the three moments equation, the matrix can be arranged as 2*L1*MA+L1*Mb+ 0*Mc+0*MD= -6*(P1*L1^2/16) -6*(W1*L1^3/24), at the right side of the equation.
We consider a column matrix 4×1, which is the load’s column (W1 W2 W3 W4), so (-6/24)=-1/4*L1^3.The row matrix 4×1 is(-1/4*L1^3 0 0 0).
For the concentrated load matrix, it has a column vector, 4×1 (P1 P2 P3 P4), and a row vector, 4×1 (-3/8*L1^2 0 0 0).
This row will be multiplied by the vector matrix (W1, W2, W3, W4).

By leveraging the three-moment equations, engineers can accurately determine reaction forces at joints.
We have completed writing both sides of the matrix equation for the moment at joint A.
The three-moment equations for the continuous joint B.
From the next slide, we will write the moment’s equation at joint B for the three-moment equations.
We have two beams at B. One is located on the left side, with length L1, and is loaded by a uniform load W1 and a concentrated load P1.
The second beam, on the right side of B and with length L2, is loaded with a uniform load W2.
The moment at B is written as MA*L1+2*MB*(L1+L2)+MC*(L2) =-6*r-br-6*r-bL, where r-bL is the elastic reaction at B from the left part, while r-br is the elastic reaction at b from the right part.
The elastic reaction at b from the left, r-bL=elastic reaction from the uniform load W1+ elastic reaction from the concentrated load P1, the elastic reaction at B from the right, and the r-br=elastic reaction from the uniform load W2. -6*(r-br)=-6*(W2*L2^3/24).
-6*(r-bL)=-6*W1*L1^3/24+(-6)* (P1*L1^2/16).
We will create a matrix as follows: the moment vector matrix is (MA, MB, MC, MD).
From the three moments equations, we have a row matrix 1×4,(L1 2(L1+L2) L2 0) to be multiplied by ( MA MB MC MD).

The Elastic reaction related to W1, W2, W3, W4, can be represented as a row matrix, 1x 4, as shown, (-L13^3/4 -L2^3/4 0 0).
While for the column matri,x due to concentrated loads being 4×1, (P1 P2 P3 P4), we have a row-column 4x,1 which is (-3/8*L1^2 0 0 0 ).
The three-moment equations for the continuous joint C.
From the next slide, the moment at joint C can be represented by the two beams intersecting at C.
The second beam is loaded by W2, with span L2, while the third beam is loaded by W3, with span L3. The three moments equations to be written as MB*L2+2*MC*(L2+L3)+MD*0= -6r-cL-6*r-cr= -1/4*W2*L2^3-1/4*W3*L3^3. We have a row matrix 1×4, (0 L2 + 2*(L2 + L3) 0), and a vertical matrix, MA, MB, MC, and MD.
For the row matrix 4×1,(0 -L2^3/4 -L3^3/4 0), and a column matrix (W1, W2, W3, W4).

We do not have any elastic reaction values from the concentrated loads, which can be represented by the row matrix 1×4 (0 0 0 0) and the column matrix (P1 P2 P3 P4).
The three-moment equations for the end joint D.
From the next slide, three-moment equations.
We are left with the moment at joint D. The elastic reaction at D=0, the moment at D=0, since joint D supports. The row matrix 4×1,(0 0 0 0) and a column matrix (W1 W2 W3 W4) Plus the row matrix 4×1,(0 0 0 0) and a column matrix (P1 P2 P3 P4). This matrix is written for the condition in which the last support is a hinge.
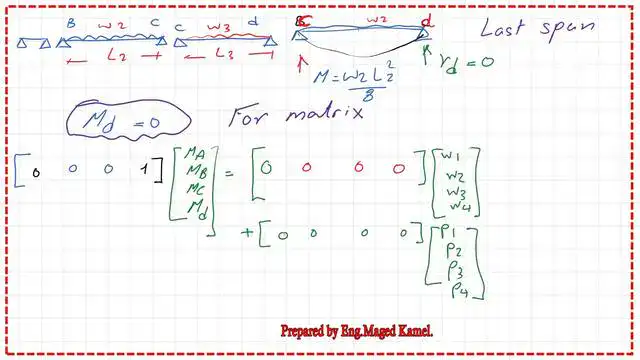
Understanding the principles behind three-moment equations is crucial for accurate structural analysis.
The final form of the matrix equations for continuous beams.
We have a 4×4 matrix multiplied by a column vector (MA, MB, MC, MD), and that matrix contains the data related to the span lengths. While at the right-hand side, we have the coefficient of elastic reactions 4×4, multiplied by the column vector (W1 W2 W3 W4) plus the coefficient of elastic reactions 4×4, P3 P4).

This is a link to the previous post 38a-Solved problem 10-1-design of steel continuous beam-2-4.
In the next post, we will determine the final values of the moments.
The PDF file for this post can be reviewed or downloaded from the following document.
Provide more information about the structural analysis – III.
Here is the link to Chapter 8 – Bending Members, section, A Beginner’s Guide to the Steel Construction Manual, 14th ed.
Here is the link to Chapter 8 – Bending Members, section, A Beginner’s Guide to the Steel Construction Manual, 15th ed.
Here is the link to Chapter 8 – Bending Members, section, A Beginner’s Guide to the Steel Construction Manual, 16th ed.