3-Part 1 of Practice problem-7-32 Discontinuity Functions

Part 1 of Practice problem-7-32 Discontinuity Functions.

We will solve practice problems 7-32, which involve developing load function expressions for W(x), shear function V(x), and moment function M(x) using the discontinuity function.

The practice problem is included in Prof. Timothy Philpot’s book An Integrated Learning System, Mechanics of Materials. The same practice problem is on pages 7-56 in the third edition.

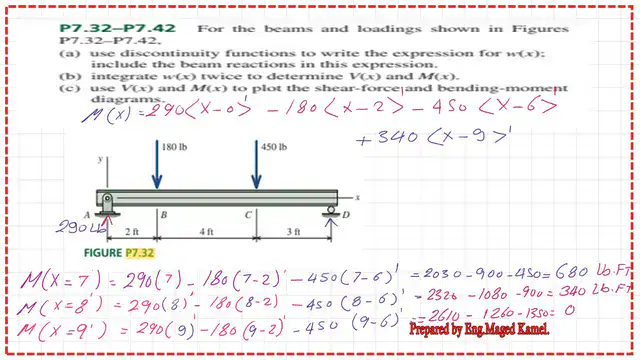
We have a given beam spanning 9 feet acted upon by two concentrated loads: P1 = 180 lb, and the second concentrated load is P2 = 450 lb. The two loads act downwards.

Part a) requires using the discontinuity function to write the expression for load w(x), the beam reactions in the expression.

In part b), w(x) must be integrated twice to determine the V(x) and M(x).

In part c), V(x) and M(x) must be used to plot Shear force and bending moment diagrams.

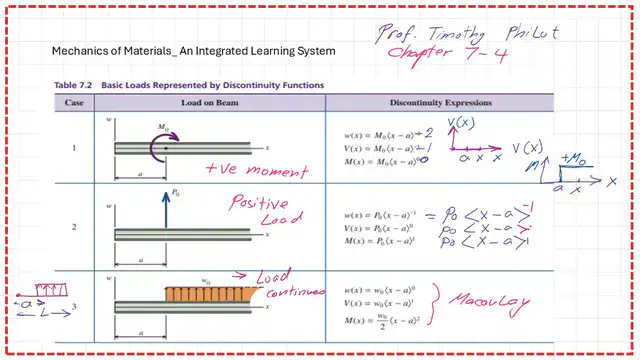
 What is the case in the discontinuity table that covers our Practice problem 7-32?

In the next slide image, we can find the second case, where the beam is acted upon by a vertical load covering our practice problem 7-32

Find the beam reactions for Practice problem 7-32.

First, we draw the free body diagram for the beam, which includes two reaction forces for the hinged support A: Ax and Ay. Meanwhile, support D, a roller support, has only one reaction: Dy.

We are using the three equations of equilibrium: ∑X=0, ∑Y=0, and ∑M=0. We are following the standard rule for directions. For horizontal loads, the positive direction is to the right.

For vertical loads, the positive direction is to the upward direction. For moments, the positive direction is the anticlockwise direction. We do not have any acting horizontal loads, so Ax=0.

 From ∑ Y=0, Ay +Dy=180+450=630 lbs.

From ∑M=0. Take a moment for all forces about the right support D, multiplying each force and reaction by the arm length to support D and considering the directions of moment rotations. -Ay*9+180*7+450*3=0. Ay value equals 290 Lb with a positive sign that includes that the upward direction is the correct sign. From ∑ Y=0, Dy=630-290=340 Lb, acting upwards.

Write the three expressions for w(x), V(x), and M(x).

In the next slide, we are ready to write the expression for W(x) for the given beam; this is case 2 from the discontinuity table discussed in the previous video.

Take the left point A as your 0,0 point, the horizontal axis X, while the Y-axis will be W(x). Following the positive direction, the upward direction for positive loads is essential.

The reaction Ay is upward, so it is positive, acting at x=0, so we write 290*<x-0>^-1 since we are dealing with load intensity.

After two feet comes a downward load of 180 lb, so the expression is -180*<x-2>^-1.

At x=6 Ft, there is another downward load of 450Lb; its expression is  -450*<x-6>^-1.

Finally, the Dy of 340lb acts at x=9 ft. The W(x)=290*<x-0>^-1-180*<x-2>^-1-450*<x-6>^-1+340<x-9>^-1.

We will ignore the last reaction while calculating will be ignored since it represents a step function for distance >9 ft.

The next step is integrating one to get the V(x) for shear.

So  V(x)= 290*<x-0>^0-180*<x-2>^0-450*<x-6>^0+340<x-9>^0.

We have integrated by adding only n+1 to all minus ones.

Again integrate to get the value of M(x)= 290*<x-0>^1-180*<x-2>^1-450*<x-6>^1+340<x-9>^1. Then, we have completed the two parts, A and B.

The shear values are based on V(x) from x=0 to x=5 feet.

In the next slide, we write the V(x) expression.

For values bigger than a, the term<x-a> is a positive raised to the power of zero equals 1. While for values <x-a> less than a, the negative value will be treated as a zero.

If the x-a is a negative value, it will be equated to zero.

 V(x)= 290*<x-0>^0-180*<x-2>^0-450*<x-6>^0+340<x-9>^0.

For <x-0>^0, 0 plus will be equal to 1.

<x-2>^0, if x is less than 2 will be considered zero while if x>2 will be positive.

<x-6>^0, if x is less than 6 will be considered zero while if x >6 will be positive.

<x-9>^0, if x is less than 9 will be considered zero while if x >9 will be positive.

There are two steps at x=2 feet and x=6′ for shear values.

We consider x=0 plus, so V(x=0 plus)=290*1=290 lb.

We consider x=1 ft, so V(x=1)=290*1-180*(1-2)^0=290-0-450*(1-6)^0=290 lb.

We consider x=2 ft, so V(x=2)=290*(2-0)^0-180*(2-2)^0-450*(2-6)^0=290-0-0=290 lb.

We consider x=2 plus, so V(x=02 plus)=290*2-180*(+ve)^0=110 lb.

We consider x=3 ft, so V(x=3)=290*(3-0)^0-180*(3-2)^0 -450*(3-6)^0=290-180-0=110 lb.

We consider x=4 ft, so V(x=4)=290*(4-0)^0-180*(4-2)^0-450*(4-6)^0=290-180-0=110 lb.

We consider x=5 ft, so V(x=5)=290*(5-0)^0-180*(5-2)^0-450*(5-6)^0=290-180-0=110 lb.

Values for v(x) for x=6,7,8 and 9 feet.

The next slide finds V(x) values for 6 FT,7,8, and 9 Feet.

We consider x=6 ft, so V(x=6)=290*(6-0)^0-180*(6-2)^0-450*(6-6)^0=290-180-0=110 lb.

We consider x=6+ ft, so V(x=6+)=290*(6-0)^0-180*(6-2)^0-450*(6+-6)^0=290-180-450=-340 lb.

We consider x=7 ft, so V(x=7)=290*(7-0)^0-180*(7-2)^0-450*(7-6)^0=290-180-450=-340 lb.

We consider x=8 ft, so V(x=8)=290*(8-0)^0-180*(8-2)^0-450*(8-6)^0=290-180-450=-340 lb.

We consider x=9 ft, so V(x=9)=290*(8-0)^0-180*(8-2)^0-450*(8-6)^0+340*(9-9)^0=290-180-450=-340 lb, which is numerically equal to By value but negative since it represents the shear value.

The moment values are based on M(x) from x=0 to x=6 feet.

In the next slide, we write the expression for M(x). M(x)= 290*<x-0>^1-180*<x-2>^1-450*<x-6>^1+340<x-9>^1.

For values bigger than a, the term<x-a> is a positive raised to the power of one. While for values <x-a> less than a, the negative value will be treated as a zero.

We consider x=0, so M(x=0 )=290*(0-0)^1=0 Lb.Ft.

We consider x=1 ft, so M(x=1)= 290*(1-0)^1=290 Lb.Ft.

We consider x=2 ft, so M(x=2)=290*(2-0)^1-180*(2-2)^1-0=290*2-0-0=580 Lb.Ft.

We consider x=3 ft, so M(x=3)=290*(3-0)^1-180*(3-2)^1-0=290*3-180=690 Lb.Ft.

We consider x=4 ft, so M(x=4)=290*(4-0)^1-180*(4-2)^1-0=290*4-180*2=800 Lb.Ft.

We consider x=6 ft, so M(x=6)=290*(6-0)^1-180*(6-2)^1-0=290*6-180*3=1020 Lb.Ft.

The moment values are based on M(x) from x=7 to x=9 feet.

In the next slide, we find M(x) values for 7,8 and 9 Feet. We consider x=7 ft, so M(x=7)=290*(7-0)^1-180*(7-2)^1-450*(7-6)^1=2030-900-450=680 Lb.Ft.

We consider x=8 ft, so so M(x=8)=290*(8-0)^1-180*(8-2)^1-450*(8-6)=2320-1080-900=340 Lb.Ft.

We consider x=9 ft, 290*(9-0)^1-180*(9-2)^1-450*(9-6)-0=2610-1260-1350=0 Lb.Ft.

This is the end of Part 1 of Practice problem-7-32 Discontinuity Functions.

The previous post is the Discontinuity Functions Table.

There is a video for this post; this is the link.

This is a link to my “ YouTube playlist” for Singularity functions.

The next post is post 3a: Part 2 of Practice problem-7-32 Discontinuity Functions