Last Updated on April 6, 2025 by Maged kamel
Moment Redistribution For Continuous Steel Beams.
Elastic redistribution for Moment values.
The design of continuous beams is a new subject. The first method is the elastic method of moment redistribution, or the 0.90 rule. We will introduce different types of beams with continuous span and fixed end moment. We will see the values of moments before and after the redistribution.

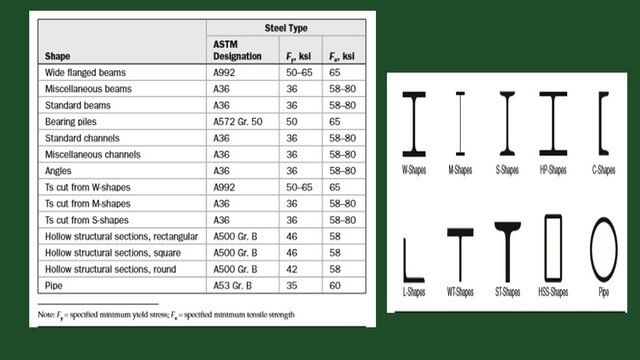
Let us have a look at the shapes W-shapes, M shapes, S-shapes, Hp-shapes, and c-shapes, L-SHAPES, wt-shapes, HSS-shapes, and pipe-shapes, and the ASTM designation, the values of both Fy and Fult for each of these shapes. For instance, for a wide flanged beam, Fy=50-65 ksi is based on the steel of A992, and for hollow structural sections, it is rectangular, Fy=46 ksi.
This is a brief revision of the values of Fy and Fult for the different types of ASTM.
The following image shows the continuous beams’ shear and moment values with three equal spans under a uniformly distributed load.

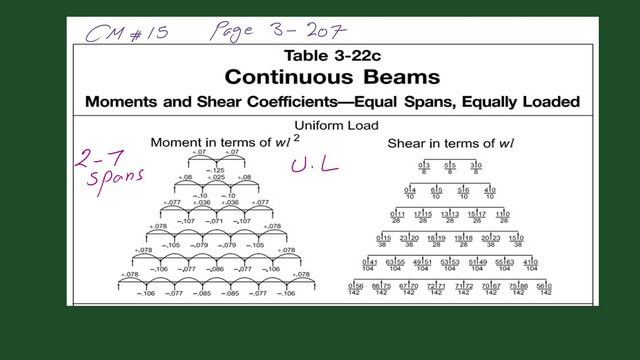
We can refer to Table 3- 22c for different types of continuous spans, from 2 to 7 spans, and the corresponding values of shear and moment under distributed load.
The code requirements for the redistribution of moment.
The AISC code permits utilizing this moment by redistributing it. Chapter B of the specification shows this procedure under clause B3.3. Please refer to the following slide images for more details.

The structural analysis for the applicable load combination shall determine the required strength of the structural members and connections based on section B2.
As we will see later, we can deduct 10% of the negative moment’s value and add this value to the positive moment based on the position of the maximum moment value. The required yield stress is not to exceed 65 ksi.

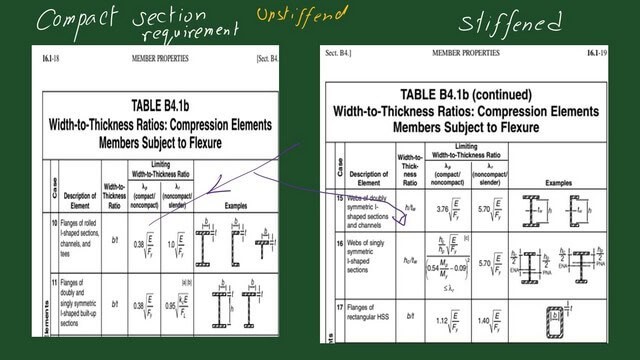
The clause shows that the steel section of the beam must be compact, following the requirement of section B4. Please refer to the following slide image for unstiffened and stiffened sections for lambda p values.
The following slides show the data of clause F13-5 for the requirement of lm , the distance between bracings to allow for moment redistribution.


The AISC has stated that the length between bracing should not exceed lm to allow redistribution. Most of the solved problems consider that the beam has continuous bracing. In the Appendix for plastic analysis and design, Professor Segui discusses the formula F13-8 by introducing a solved problem A-2.
The next slide shows the details of the equation of clause F13-8 for the Lm value.

How do we perform redistribution?
We will introduce a continuous beam with two equal spans; the acting load is uniform. The following slide image shows the moment values before and after redistribution.
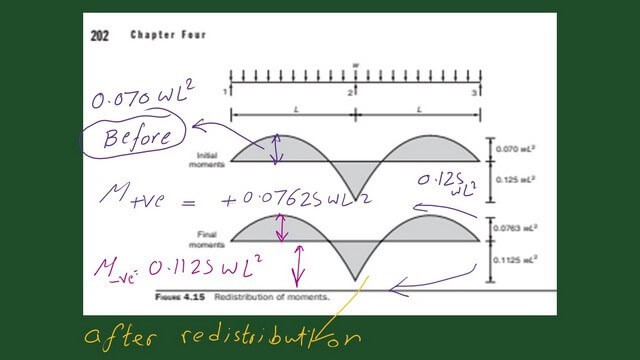
The maximum bending moment is 0.125 wl2, which is bigger than the positive value, which is 0.07 wl2. We will deduct 10% from the negative value, so the final value will be 9/80 wl2.
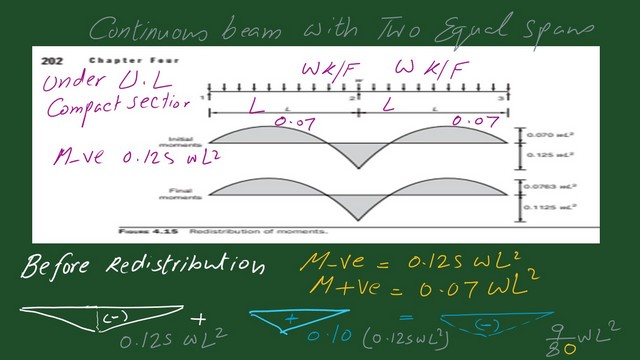
We add 0.5 of the 0.1*0.125 Wl^2, since the position of the maximum moment is at the midpoint of the first span. The final positive value equals 0.07625 Wl^2. Please refer to the following slide image.

Elastic moment distribution for a fixed-end beam with central load.
We will now review the case of a fixed-end moment with one span and a central point load. This sketch shows the fixed-end beam’s shear and bending moment values.
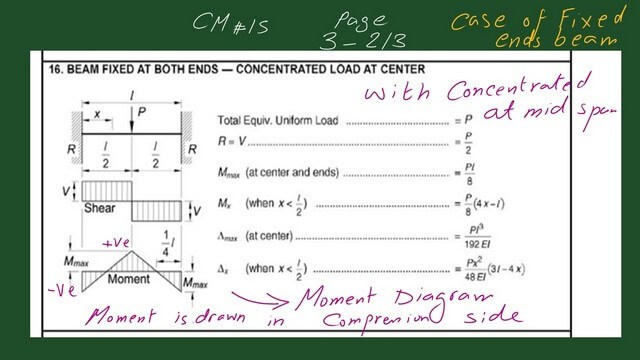
The values of positive and negative moments are the same, which is wl^2/8. The final negative moments equal 0.1125 PL, and the final positive value equals 0.1375 PL.
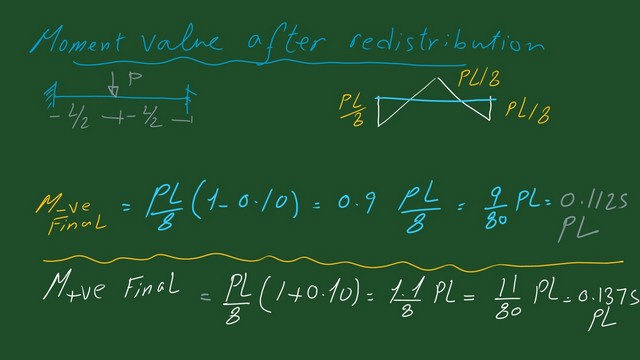
Elastic moment distribution for a fixed-end beam with a uniform load.
The following image shows a fixed-end beam’s shear and moment values with a uniformly distributed load.
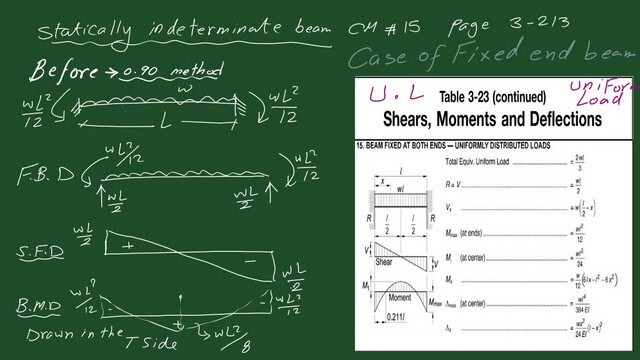
Deduct 10% of the fixed-end moment value, and the final value of the fixed-end moment beam will be WL^2/40.
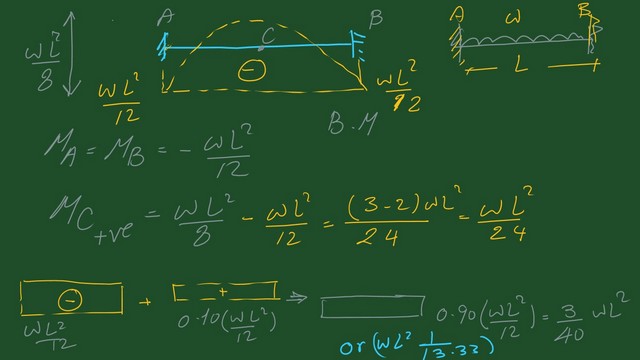
The positive bending moment before redistribution is equal to 0.07 wl^2. After a moment redistribution will be increased by 0.10*(w*L2)/12=0.00833 WL2. The slide image shows the moment’s value after using the 0.90 rule.

The next post solves Problem 4-15. It includes how to design a continuous beam of two spans and is considered an application for moment redistribution.
For a useful link about the distribution of continuous beams.