Last Updated on December 10, 2025 by Maged kamel
We will introduce practice problems for a trapezium. Two practice problems for inertia for a trapezium are 8.41 and 8.47. These problems are quoted from BEDFORD’s Engineering Mechanics statistics.
Two Practice problems for inertia for a trapezium.
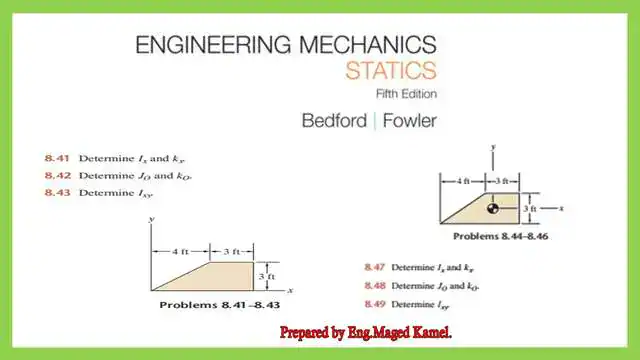
The following slide shows problems 8.41-8.47, which are the subject of our recent post.
The first practice problem for inertia is 8.41. Find Ix and kx for a given trapezium.
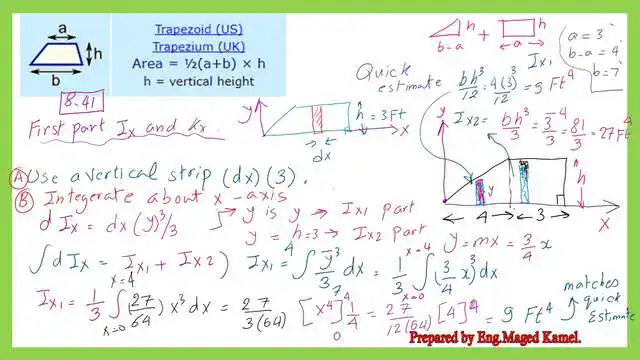
A quick estimate of Ix for a given trapezium.
For the first of the two Practice problems for inertia, we have a trapezium with a base length of 7 feet and an upper part length of 3 feet. We must determine the moment of inertia Ix and the radius of gyration Kx.
We have a quick answer for the moment of inertia, as we can see from the upper right corner of the next slide image: the trapezium consists of a triangle of base (b-a) equal to 4 feet with height h equal to 3 feet, and a rectangle of base a equal to 4 feet with height h = 3 feet.
From our previous posts, we have the expression for triangle inertia about the base as Ix = base *height^3/12, which is equal to (4*3^3/12)=5 Ft4.
At the same time, the inertia for a triangle equals the base *height ^3/3, which equals (3^4)/3=81/3=27 ft4. Then, the moment of inertia for the trapezium is 9+27=36 feet4.
Ix for a given trapezium by integration using a vertical strip.
As shown in the next slide, we can use a vertical strip of height y and width dx. The inertia of this strip about the X-axis is the sum of two inertias. The first inertia is dIx1 plus dIx2
To find the value of y, we can determine the equation of the triangular line as y = 3/4 x, while for the rectangular section, y equals h, which is 3 feet. The expression for dIx1 is dIx1 = (dx * y^3 / 3). This expression can be rewritten as dIx1 = 1/3 * (3/4 x^3) * dx.
The integration is from x=0 to x=4. The Ix1 value equals 9 ft4, which matches the previously estimated inertia for the triangular part.
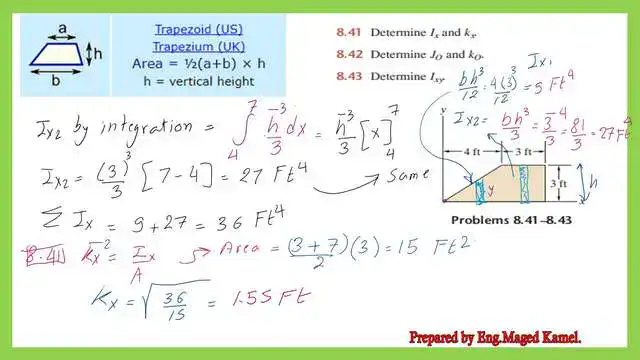
Integrating the vertical strip from x=4 feet to x=7 feet gives the value of Ix2 for the rectangular portion.
The inertia of the strip about the X-axis is dIx2 =(dx)*(h^3/3), the h value is 3 Ft, and the final value is Ix2, which will be found to be equal to 27Ft4.
The Total Ix value is 36 Ft4. The square of the radius of gyration equals Ix/A=36/15. Then the radius of gyration kx equals 1.55 Ft.
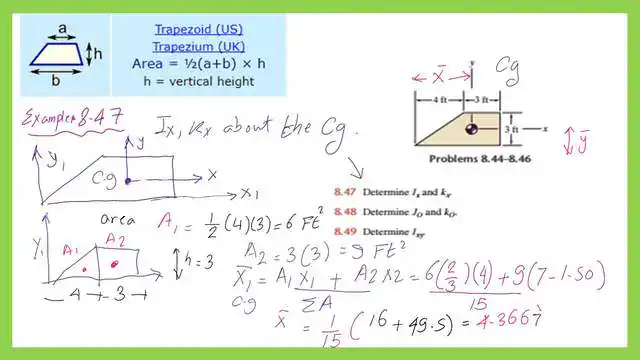
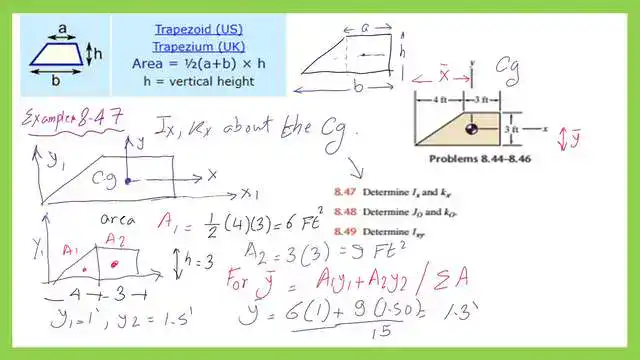
The second practice problem for inertia is 8.47. Find Ix and kx for a given trapezium about the Cg.
For the second practice problem, 8.47, for inertia, you must find the moment of inertia for the trapezium at the Cg and determine the hex value.
The same Trapezium, with a base length of 7 ft and an upper part length of 3 ft, is dealt with.
Determine the x-bar for the Trapezium.
We need to find the area and the x-bar, or the horizontal distance from the Cg to the vertical axis y1, passing through the left point of the trapezium. Later, we will use this information for the forthcoming practice problems.
Use the expression of A(X bar)=(A1*X1+A2*X2), A1=6 ft2, while A2 equals 9 ft2. The X1 is the horizontal distance from the Cg of the triangular part to the axis y1. The value is (2/3)*4=8/3 Ft.
While X2 is the horizontal distance from the Cg of the rectangular part to the axis y1.
The x2 value equals (7-1.50)=5.50 ft. Using the expression A(X bar)=(A1*X1+A2*X2), and substituting for the known values, we can get x bar as equal to 4.3667 Ft. Please refer to the details of calculations in the next slide image.
Derive a general expression for the Ix value.
If you wish to derive a general expression for Ix of the trapezium. The Ix is the sum of Ix1 and Ix2. For Ix1 we can write its expression as equal to the integration from 0 to (b-a) of x^3*dx*(h^3)/3*(b-a)^3.
Proceeding with the integration will give us h^3/12*(b-a). While for the integration of Ix2, or the rectangular portion, is the integration from (b-a) to b of (dx*(h^3/3), and its final value is a*h^3/3.
Adding Ix1 to Ix2 will give us (h^3/12)*(3a+b). Substitute to get Ix equal to 36 Ft4.
Determine the y-bar for the Trapezium.
We need to find the value of the area and Y bar, or the vertical distance from the Cg to the trapezium base. Use the expression of A(y bar)=(A1*y1+A2*y2), A1=6 ft2, while A2 equals 9 ft2.
y1 is the vertical distance from the triangular part’s Cg to the trapezium’s base. Its value is (1/3)*3 = 1 Ft.
y2 is the vertical distance from the rectangular part’s Cg to the trapezium’s base. The value is (1/2)* 3 = 1.5 ft. We can set y bar equal to 1.3 ft.
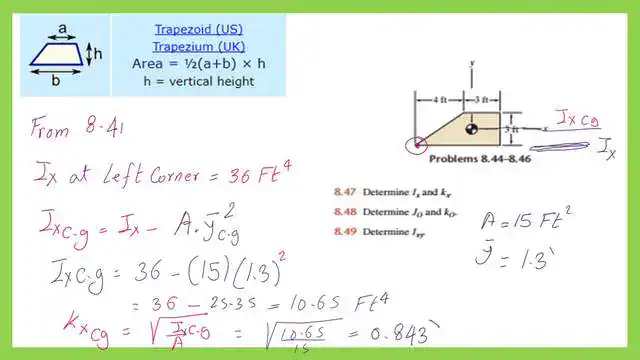
Determine the final value for Ix at the Cg for the Trapezium.
The final value of Ix at the cg is equal to the value of ix about the base minus the product of the trapezium area by the square of y bar distance.
From the estimated data, we have Ix = 36 ft4, while the area of the trapezium is 15 ft2. The y bar of the trapezium is equal to 1.3 ft. Applying the expression for Ixcg, we obtain a value of 10.65 ft4.
The radius of gyration at the Cg is equal to the square root of Ixcg/area and is equal to 0.843 ft.
Derive a general expression for Ix at the Cg value.
If you wish to derive a general expression for Ix at the Cg of the trapezium, we can use the general expression of Ix for the trapezium. As a reminder, the Ix value equals h^3/12*(3a+b) and deducts the product of area *y bar cg^2.
Please refer to the next slide image for more details. We can get the final expression as Ixcg =(h^3/(36)*(a^2+4*a*bn+b^2)/(a+b).
We can use the known values a = 3 feet, b = 7 feet, and h = 7 feet and substitute Ix cg in the final expression. Finally, we get the value of Ixcg equals 10.65 ft4.
Thanks a lot, and I look forward to seeing you in the next post, on 26, Two Practice Problems for Polar of Inertia for Trapezium.
Please refer to post 22 for more information about Iy for a trapezium.
Please refer to post 19 for more information about Ix for a trapezium.
The following post is post 26-Two, Practice problems for the polar of inertia for trapezium.
Please refer to this link for a valuable external resource on the parallelogram’s area, Cg, and inertia.