2-How to determine x bar for a right angle-case-1?

How to determine x bar for a right angle-case-1?

The difference between case-1 and case-2- for the right angle triangle.

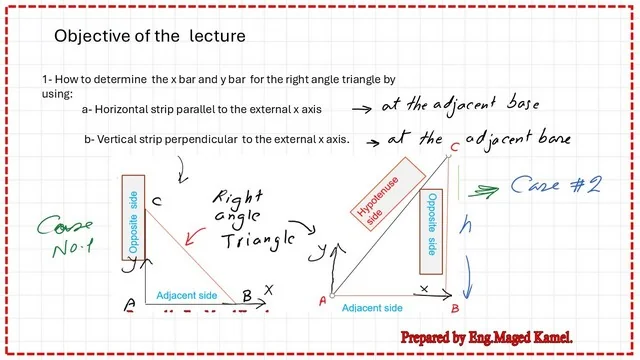
The first moment of area for the right angle triangle case-1 and how to determine the x bar value? will be the case of the right-angled triangle.

We have two cases case-1 for which the opposite side of the triangle is to the left side and the base is at the bottom of the hypotenuse on the left side. While for case no.2, we have the opposite side of the triangle to the right side and the base at the bottom of the hypotenuse on the left side.

The difference between case-1 and case-2 can be shown in the next slide image.

Using a horizontal strip to get x bar for a right angle case-1.

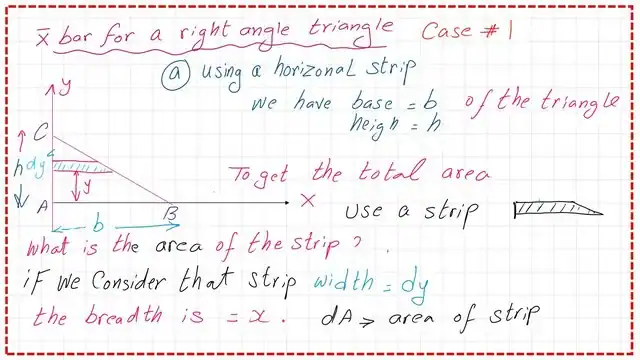
We will start by using a horizontal strip to get the value of the X bar or the Cg horizontal distance to the y-axis.
We have X and Y axes respectively and the base of the triangle. We have line AB with the length of b, the rise of the triangle is=h, and the inclined portion AC, equation: y =mx+C m which is a slope is equal to -h/b *x, and the intersection with y-axis =h. The horizontal strip is shown in the next slide image.

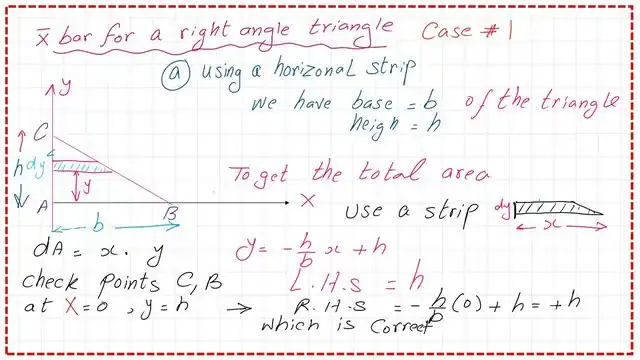
That’s why the AC equation is Y =-( h/b) *x+h. The horizontal strip thickness is dy and the length is x as shown in the next slide image.

First, it is good to examine the equation of the inclined line BC By substituting the value of x=0 which is point C and check that the corresponding y value=h, when using the equation y=-(h/b)x+h). We have Y=h when x=0.

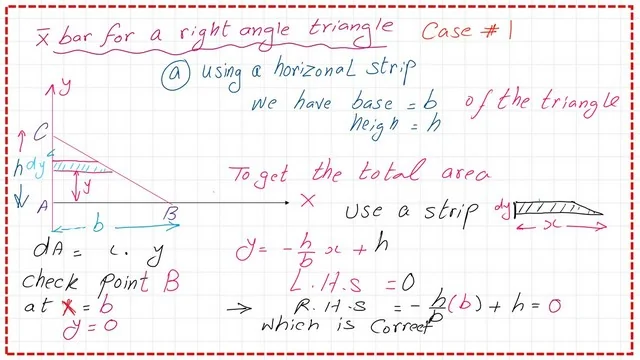
For the second point which is point B, when the horizontal distance x=b, and the corresponding y value=0.

Perform integration for the horizontal strip to get the area of the right-angle triangle.

The area of the triangle is the summation of all the tiny horizontal strips, which can be expressed by using the integration for the strip from the start which is y=0 to the end which is y=h, considering moving the strip in the vertical direction.

Since the strip width is x and its height is h, we are going to use the relation by y and x as derived from the equation of line BC.
We will estimate the area DA as the product of x*dy, since integration is in the vertical direction. We will omit x expression by substituting it value in terms of y. the x value=(h-y)/h*(b).

Perform integration for the horizontal strip to get the first-moment area about the Y-axis.

The expression of the dA*x-strip will be represented by the first moment of area about the y-axis, where the x-strip is the horizontal distance from the Cg of the strip to the y-axis. The expression of dA*x-strip is shown in the next slide image and integration will be carried out in the vertical direction from y=0 to y=h.

The final A*x bar represents the product of total area * the horizontal CG distance from the y-axis will be found as in our case=b^2*h/6, where b is the triangle base while h is the height.

X bar for a right-angle final step.

X bar value will be obtained by simply dividing the first moment of area /Area. We will get x bar for a right angle=b/3 or one-third of the base width.

This is the link to to download the pdf used for the illustration of this post.

For a good external reference, please refer to the following link.
This is the link to the next post is -X bar for a right angle-case-1-using vertical strip.