2- Easy approach to solved problems for net area estimation.

Solved problems for net area estimation. 

How do we estimate the net area for plates?

A solved Problem 3-1.

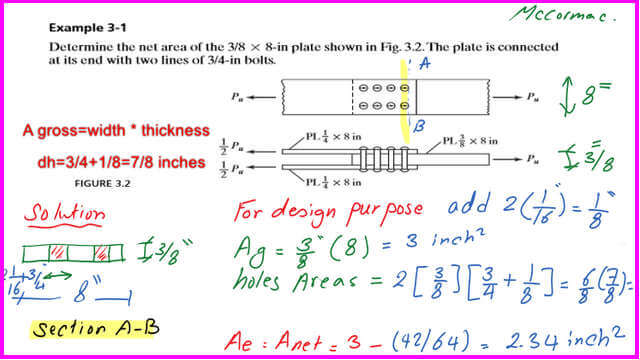
In solved problem 3-1, we have a plate 3/8 inch thick and 8 inches wide.
Determine the net area of the 3/8-inch x 8-inch plate, which is connected at its end with two lines of 3/4-inch bolts.

This is the original plate, 8 inches by 3/8 inches, connected with two thin plates. Each has an exact width of 8 inches and a thickness of 1/4 inch.

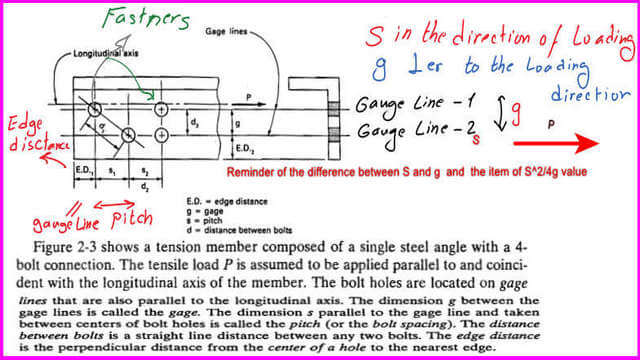
This is the first gauge line in the direction of the longitudinal tension, which is in the direction of the applied force, and this is the second gauge line.
As discussed earlier, the distance between the two center lines at the longitudinal direction represents the gage distance, while the perpendicular distance is the pitch.
We don’t have a zigzag line, so we will deal with the vertical section, as seen in the next slide image. The next image shows the difference between the s and g distances for the bolted connection.

The area net, while selecting a vertical line AB= Ag – the area of bolts.
1-The bolt diameter as given =3/4 inch. We will refer to Prof. McCormac’s remark while considering the diameter of the bolts by adding 1/8 inch to the given diameter of the bolt.

While drilling for the bolts, damage to the material will cause an extra dia of 1/16 inch, plus the 1/16 inch, so the total added will be 1/8 inch.

2-After drawing sections A and B, the width is 8 inches, the thickness is 3/8 inches, and there are two bolts.
We estimate the final diameter of the bolt as (3/4+1/8)=7/8″ inch. There are two bolts.

3-The A gross=3/88=3.00 inch2, for the net area Anet we deduct the area of the two holes, then Anet=Ag-sum(d)t=3.00-2(3/8)(7/8)=2.34 inch2. for U=1, then A eff=1*2.34=2.34 inch2.

This is a list of the equations used to estimate the limit state of Yielding and limit state of fracture for tension members.

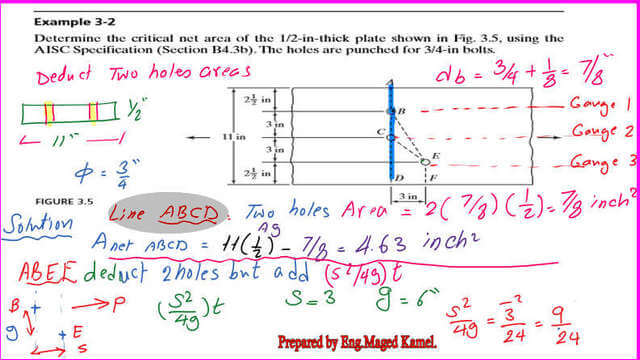
Problem 3-2-determine the critical net area for a plate.

This is the second problem 3-2. It requires estimating the critical net area of a 1/2-inch thick plate for bolts with a diameter of 3/4 inch.

We have two paths to failure. The first path is ABCD. In this path, we will deduct two holes, and there is no zigzag line. 

1-The area gross Ag=111/2=5.50 inch2, for Anet=Ag-sum(d)t=5.50-2(1/2)(3/4+1/8)
=5.5-(7/8)=4.63 inch2.

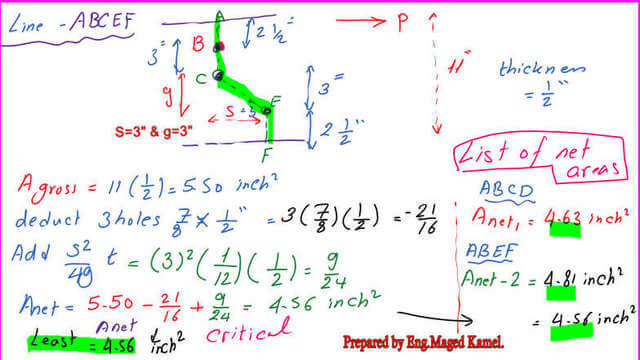
For the second path, which is a staggered line path ABEF, in this path, we are going to deduct two holes and also consider the zigzag line BE for which S=3″ and g=6″. 
  2a-The area gross Ag=11*1/2=5.50 inch2.

   2b- For the net area for the staggered line ABEF– Anet=Ag-sum(d)t+tplS^2/4g=5.50-2(1/2)(3/4+1/8)+1/2(3^2)/(46)=5.5-1/2*(7/8)+0.1875=4.81 inch2.
 

For the third path, which is path ABCEF, in this path, we will deduct three holes and consider the zigzag line CF for which S=3″ and g=3″. 
   3a-the area gross Ag=11*1/2=5.50 inch2.  

3b- for Anet=Ag-sum(d)*t+tpl*S^2/4g=5.50-3*(1/2)*(3/4+1/8)+1/2*(3^2)/(4*3)=5.5-1.3125+0.375=4.56 inch2. Finally, the least net area will equal 4.56 inch2; the final route selected is ABEF.
 

That is the end of the problem- 3-2. Thank you all.
For more problems, please refer to the following external link.
For the next post, A Solved problem 3-1 for the nominal strength.

See Chapter 3, Tension Members, and Bartlett Quimby for a useful external link.