Last Updated on July 30, 2026 by Maged kamel
- How to solve for x-y by L-U Decomposition?
- Illustration using the Gauss elimination method for the U matrix formation.
- Can we use an elementary matrix to get the L and U matrices?
- Write an expression of (L*C)=b as the first step to developing an expression to solve for x-y for two equations-L-U.
- Find the inverse of the L matrix as the second step to solve for x-y by L-U decomposition.
- Get the value of C as the third step to develop an expression to solve for x-y by L-U decomposition.
- Get the value of X as the fourth step to solve for x-y by L-U decomposition.
- A quicker way to get X and Y values.
How to solve for x-y by L-U Decomposition?
I have prepared a video that illustrates the post’s content
.
The Timestamps for the video are shown.
The next slide shows the content of post 3- Numeric Linear.
Illustration using the Gauss elimination method for the U matrix formation.
We have a matrix A with two rows and two columns, given by (2 3 3 4). How to develop the upper matrix U for matrix A?
We use Gauss elimination with elementary row operations to convert the matrix A into an upper-triangular matrix, and then use back substitution to solve for the values of the unknowns.
For matrix A 2×2, which is given as (2 3 3 4). To convert this matrix into an upper matrix, we want the diagonal to be nonzero and set a21 to zero.
Using a11 as a pivot, divide a21/a11 by the minus sign by R1, and add the result to row R2. The second row R2 will be changed.
We will have a new second row as (0- ½). As we have noticed, there was no operation in the first row of matrix A, which is the same as in the upper matrix. Element U22, second row /2nd column is equal to (a22-(a12/a11).
What about the Lower Matrix? We have, by definition, L11 = L22 = 1 and L12 = 0. For L21, it equals (a21/a11), given that a11 is a pivot. By placing the result in a new second row, we can obtain a zero value for U21, the first element in the second row and first column.
If we want to check whether L*U multiplication yields (2 3 3 4), we can use row-column multiplication. (1*2+0*0)=2, and (1*3+(0*-1/2)=3. (3/2*2+1*0) =3+0=3 which we will lead us to 3 and (3/2 * 3+1*(-1/2)=4.50-0.50=4. We have a valid L*U through a valid multiplication. We will use the same matrix A to solve for the values of two unknowns, x and y.
Now, the A matrix, as the product of L*U, is shown using matrix symbols.
Can we use an elementary matrix to get the L and U matrices?
We can get the values of L and U matrices for the given matrix A, but first, we get the U matrix by multiplying matrix A by (-3/2* by the first row) and adding to the second row, and we do the same for the identity matrix. The elementary matrix will be (1 0, -1.5 1). Please refer to the following slide.
We can prove that the elementary matrix is the inverse of the lower matrix L.
We get the inverse of the elementary matrix; the value of L is (1 0, 1.5 1) according to Doolittle’s method.
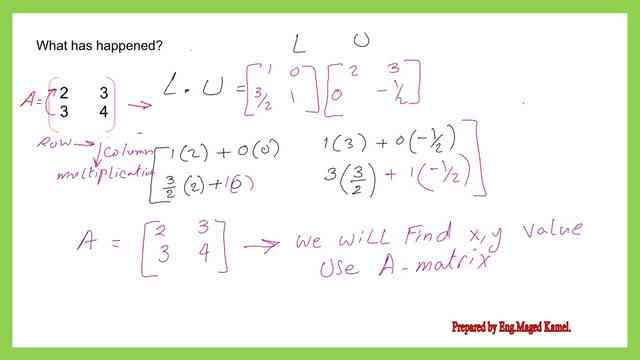
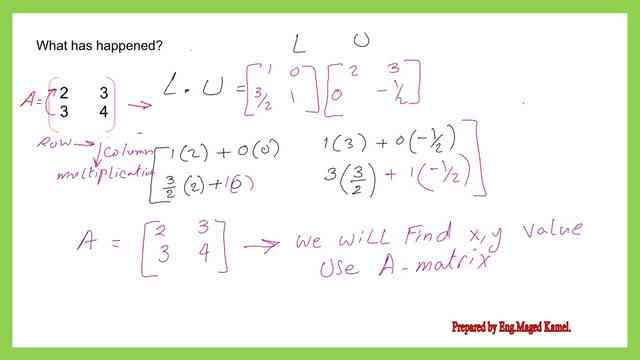
Write an expression of (L*C)=b as the first step to developing an expression to solve for x-y for two equations-L-U.
Consider the two simultaneous linear equations. The two equations can be expressed using matrices as A*X = b, where A is a 2×2 matrix in our example. Matrix X is a ( 2×1) matrix that contains (X Y), the unknown variables, while C is a (2×1) matrix of values (13 18).
We use matrix C as an intermediate stage to solve for x-y by L-U Decomposition.
Since we have expressed that matrix A is a product of(L*U), we can further write a new expression as (L*U)*X=b.
The values of L& U, and B are known; the only unknown is the column vector matrix X.
A new expression is (U*x)=C; C is a new item that is unknown. Finally, A*x = b can be expressed as (L)*C = b. To solve for a value of C, the inverse matrix of L-1 is presented and multiplied by the sides of the given equation. That process will enable us to get a value for matrix C. The modified expression is shown in the next slide image.
Find the inverse of the L matrix as the second step to solve for x-y by L-U decomposition.
In the lower matrix L, the element is (1 0, +3/2 1), then its inverse of the lower matrix is L-1, we can estimate the determinant value of l, which is =1-0=1.
We divide the adjoint matrix by the determinant. We will swap and make a change of sign of (3/2) to (-3/2), and( 0) will be the same. The final value of L-1 can be expressed as a 2×2 matrix and is = ( 1 0 -3/2 1).
Get the value of C as the third step to develop an expression to solve for x-y by L-U decomposition.
Get the value of C as the third step to develop an expression to solve for x-y by L-U decomposition. The matrix C is the product of (L-1)*(B).
Since both values are known, we can then get the value of C. Multiplying two matrices(2×2) by(2×1) will yield a new matrix with (2×1) with a value of (13 -1.5). The details of the estimation is shown in the next slide image.
Get the value of X as the fourth step to solve for x-y by L-U decomposition.
Get the value of X as the fourth step to solve for x-y f by L-U decomposition. Remember that we have the expression U*x = C; get the inverse matrix of C, which is a new 2×2 matrix. X = (U^-1)*X; then the final value of X is 2 3). The matrix (X Y) is a (2×1) matrix. The value of x=2 and y=3.
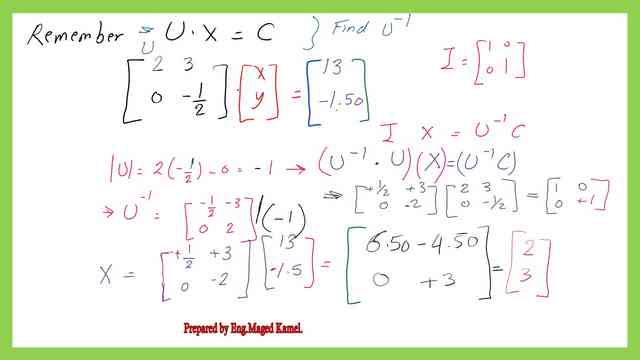
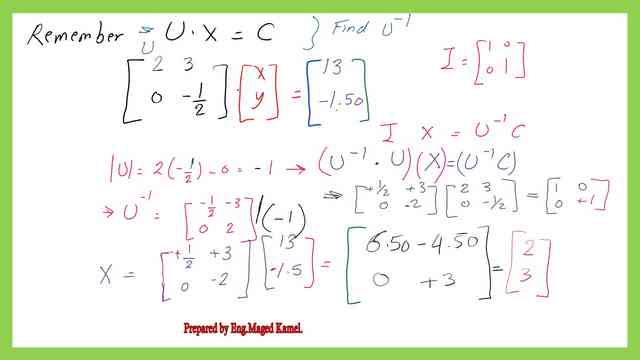
Substitute the values of x and y to check whether the x,y values are right or wrong.
After checking the two given equations, we find that the estimated values of x and Y satisfy the two equations. We have x = 2 & y = 3. In the last step, we would like to check if our solution is correct. 2x + 3x + 4y = 18.
We introduce x value as=2 and y value as 3, then (2*2+3*3)=13, which will give us the right-hand side as 13.
While 3*2+4 *3=6+12=18, which is already equal to the right-hand side of the second equation.
A quicker way to get X and Y values.
We can express X as equal to the product of the inverse of U by the inverse of L by matrix B. Please refer to the next slide for more details. This method is considered quick if you have the inverse of L and U in hand.
We use the elementary matrix to get the upper matrix U, which equals the product of E1 by matrix A. We can obtain the inverse matrix of U, as shown in the next slide. The elementary matrix can be considered as the inverse of L.
The following slide shows the final value of X and Y.
The PDF file for the post.
The following post: step-by-step on how to derive the expression for L-U values for a -3×3 matrix.
HELM-Helping Engineers Learn Mathematics.
This is the Omni calculator for estimating various items of linear algebra -LU Decomposition Calculator.
This is a link to another –Calculator for matrices.