Last Updated on June 17, 2024 by Maged kamel
Mohr’s circle of inertia-third case-part 2.
In this post, Mohr’s circle of inertia-third case-part 2, we will be interested in showing the steps to draw Mohr’s circle of inertia in the third case, where Ix is bigger than Iy and Ixy is negative. Imax value will be equal to (Ix+Iy)/2 plus R the radius of the circle. for Imin it will be equal to equal to (Ix+Iy)/2 minus R the radius of the circle. The value of negative and more than 90 degrees, the value of 2θp1 will be equal to 180- 2θp2. In the normal view, the U axis will be in the first quarter while the V axis will be in the fourth quarter as shown in the next slide image.
The steps used to draw Mohr’s circle of inertia-third case.
To draw Mohr’s circle of inertia-third case-part 2, the first two steps are to draw the two orthogonal axes. The first axis represents the Moment of inertia values, Ix, Iy, and Imax, and minimum values, while the second axis represents the values of the product of Inertia Ixy.
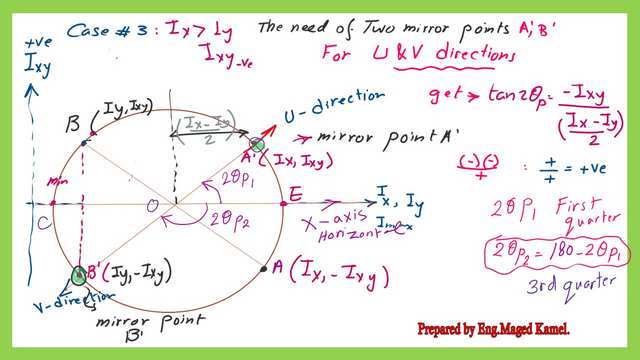
The coordinate of point A(Ix, -Ixy), -Ixy is given from the data of the case. Point B has a coordinate (Iy,+Ixy), and the value of Ixy is the negative value identical to the Ixy of point A. Locating Points A and B with their respective values of Ix and Iy, as shown in the next slide image.
Join Points A and B and get the middle point of line AB, this point is the point of the Circle center which is point O. The radius value is the sqrt( (Ix-Iy/2)^2+Ixy^2). Start from point O and draw the circle with the radius value just estimates. The circle will interest the line in two points C and E.
Point E is the maximum value of Ix and it equals (Ix+Iy)/2)+R. Point C is the minimum value of Ix and it equals (Ix+Iy)/2)-R.
We can find that line OA represents the x-axis in Mohr’s circle, while axis OB is the Y-axis in Mohr’s circle.
Need for two mirror points A’ and B’ in Mohr’s circle of inertia-third case-part 2.
In Mohr’s circle of inertia-third case-part 2 we need two mirror points. Setting point A’, which is a mirror of point A and has a coordinate of (Ix,+Ixy) and gives the direction of the maximum moment axis U. This point A’ will enable us to rotate the x-axis or line OA a clockwise rotation by the value of 2θp1. The x-axis will be horizontal; the U line will also have a new direction represented by line OA’.
Point B’ is the mirror of point B and has a coordinate of (Iy,-Ixy) and is used to indicate the direction of the V-axis, which is the direction of the minimum moment of the inertia axis.
Angle 2θp1 is the angle between the X-axis and Major axis U, which is the angle enclosed between OA and Line OE. Point E is the point of the maximum value of inertia.
Angle 2θp2 is the angle between the x-axis and Minor axis V, which is the angle enclosed between OA and Line OC. Point C is the point of the minimum value of inertia.
The direction of U and V axes in normal view using Mohr’s circle of inertia-third case-part 2.
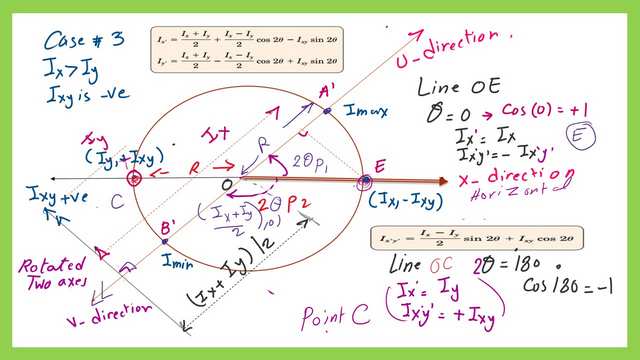
Join points OA’ to get The U-direction. Join the two points O and B’ to get the V- direction for the normal view, the view from which the x and y axes are orthogonal in the normal view. The directions of both the U and V axes are shown in the next slide image.
For the orientation of two axes Ixy and Ix, so the x-axis is horizontal, we can find that point E is the point at which Ix’ = Ix at 2θ = zero and Ix’y’ =-Ixy since the line OE is the horizontal line, while point B’ has Ix’=Iy and Ix’y’=+Ixy.
It is shown that this drawing fulfills the requirement of Case-3, that Ix is bigger than Iy and Ixy is negative. The V axis is rotated by an angle of (φp2) in a clockwise direction from axis X, While the U axis is rotated by an angle of ( 2φp1) in the anticlockwise direction from axis X.
You can refer to the first part for more information.
In the next post, we will solve a problem that covers a solved problem for Mohr’s circle of inertia-third case.
This is a link to a useful external resource. Calculator for Cross Section, Mass, Axial and Polar Area Moment of Inertia, and Section Modulus.