What is the First moment of area?
Topics are included in the illustration.
The lecture includes important definitions for the area determination and first moment of area and second moment of area and the product of inertia. A discussion of the similarity between areas and forces, how to represent an enclosed area by a group of areas, the sum of these areas will be the same as of the arbitrary area.
If we have a series of forces, we can get the resultant and the point of application, likewise, we can estimate the CG of an area and estimate the first moment of the area.
This is a brief description of the content of the lecture.


The similarity between areas and forces.
There is a similarity between forces and the areas. If we have a series of forces, please refer to statics, to get the resultant F of these forces F1, F2, F3, F4, F5. The sum of forces represented by the symbol Σ can be written as F=ΣFi for I from 1 to 5.
To get the y bar of these forces, we draw a horizontal axis X. If the distance from the outer axis to the first force F1 is X1, and similarly, the distance from this axis to the second force F2 is X2, and X3 is the distance to the third force F3, etc.
Y- bar is the distance for the resultant Force F from the external arbitrary axis = the moment produced from the Five forces/ F.


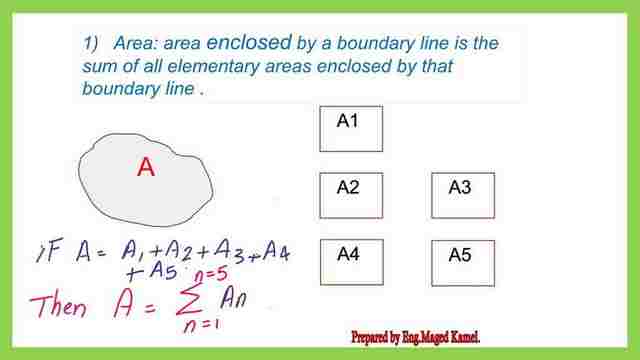
The first definition for area determination.
The first application for integration is how to estimate the area and CG of an object. Let us check the first definition. The area enclosed by a boundary is the sum of all elementary areas enclosed by that boundary line.
The same principle, as we have done with the resultant force, can be applied in the case of areas. As we can see from the next slide, if we have an enclosed area by a boundary line, it can be represented by Five areas A1, A2, A3, A4, A5. The total value of the area will be=ΣAi, for i=1 to i=5.

The second definition for the first moment of AREA.
The center of gravity is the at which the resultant of all elementary areas passes, according to the next slide, if we have five areas each area has a CG distance to an arbitrary axis, we call it axis X, the distance from Cg of A1 is y1, and the distance from CG of area 2 is y2, he distance from Cg of A1 is y1, and the distance from CG of area 32 is y3. The sum of the first moment of area, that is, (A1*y1+A2*y2+A3*y3+A4*y4+A5*y5)=A*YA, or YA is called y bar.



Y bar value for areas.
The y bar value can be estimated by dividing the first moment of the five areas by the total of these areas, so Y-bar=(A1y1+A2y2+A3y3+A4y4+A5*y5)/A is called y bar.



In case that, we use X-axis at any location, still the first moment of the area is valid if we replace the area by force.


X bar value for areas.
The sum of areas from A1 to A5 is =At, if we consider that each area has a horizontal distance from its CG to an arbitrary axis y, Again the sum of the first area of all of the five areas will be equal to At*Xbar.
Then X bar value can be estimated by dividing the first moment of the five areas by the total of these areas.
X-bar=A1X1+A2X2+A3X3+A4X4+A5*Xy5)/A.
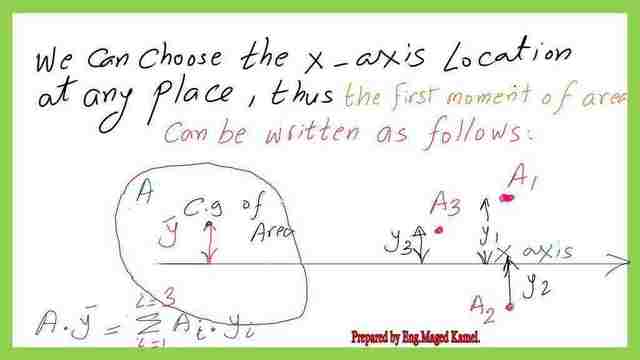

This is the case if we consider the areas as forces then we can get the x bar of these forces.


In this sketch, the areas are represented by forces that create moments about the Y-axis.


The difference between the first moment of area and the second moment of area.
The statical moment or the first moment of area is the product of each elementary area by the normal distance. This is the definition of Ax and Ay. The distance should be perpendicular to the axis since we are estimating moments.


This is the definition of the first moment of area about the x-axis and also about the y-axis.


The second moment of area.
While the Moment of inertia or the second moment of area about an axis is the product of each elementary area by the square of the normal distance from that axis. The second moment of area about the y-axis will be the product of A*X^2. While the second moment of area about the X-axis will be the product of A*Y^2.


The product of inertia.
The product of inertia is the sum of the product of each elementary area by its corresponding distances referred to in these two axes.
When we take the distance X to the y-axis, the distance y to the X-axis to estimate the product of inertia we will use the product of A*x*y. The product means the multiplication of( x*y) by the area.


The CG and area of plane shapes.
We have shapes of plane areas, in tables, we have a triangle, square, rectangle parallelogram, trapezoid, circle, ellipse, and sector.
For each shape, the area was estimated.
For instance, the area of the trapezium is 1/2* (top distance+ bottom distance )*h, where h is the height. The circle area is (π*r^2).
For the area of an ellipse, if the major axis length is a and, the minor distance is b, we notice that the”a “distance is in the x-axis direction, while “b” is in the y-axis distance. The center of the ellipse is at point (0,0). but sometimes we could have a rotated ellipse. In case the enclosed angle θ=90 degrees, we get a quarter of a circle. While for θ=180=π, we will have a half-circle shape with area=0.5(r^2π)=0.5πr^2.


This is a link for the pdf file used in the illustration of this post.
For a good external reference, please refer to the following link.
For the next post, how to determine x bar for a right angle-case-1?.

