Last Updated on September 1, 2024 by Maged kamel

What is the definition of IRR-NPV?

The new Items are Irr-Npv. The first item is the IRR, which stands for the internal rate of return. The internal rate of return is the interest rate that makes the net present value =0. The second item is NPV, or the net present value.

What is the NPV?

Net present value -NPV is the difference between the present value of cash inflows and the present value of cash outflows over a period of time.

The NPV could be positive if your investment is good; otherwise, if it is negative, your investment is bad. But in this post, we are interested in finding the rate i that makes this NPv=0. We will have two examples of the positive and negative NPV quoted from the (math is fun ) site.

The first example is that someone who wants to get an investment of 10% lends his friend $500 now, and he will receive $570 after one year. It is required to check the NPV and find out whether it is positive or not.

We draw the time scale from 0 to 1, and the vertical axis will be cash in-out. The $500 will be drawn pointing downwards since it is an outflow.

After a one-year payment of $570 is received, a vertical arrow is drawn by that value. The idea behind estimating the NPV is to return all future inflows to the corresponding present value.

These inflows will be pointing upwards. The NPV is estimated by summing all the cash in and out at time t=0. We consider i=10%. The present value of $570 is =(0.909*570); this value will be added to ($-500). As we can see in the next slide, the NPV value is equal to $18.18. The investment of 10% is achieved as required.

The second case is when the investor wants 15% as interest value.

The sample example will be used, but this time, the interest i% value will be taken as 15%. The present value of $570 is obtained and will be =(570/1.15). The NPV can be found to be =$-4.35. This value will indicate that this investment is not good.

A Solved Problem for IRR.

One invests $2000 now and receives 3 yearly payments of $100 each, and in the last year, he receives $2500. We draw the diagram as follows: $2000 is drawn downwards, Time is drawn at 0, 1,2,3 year intervals, at Time 0 $2000 is drawn downwards at the end of the first year, and $100 is drawn upwards.

The same applies in the second and third years, plus $2500 is drawn upwards at the end of the third year. We will estimate the net present value =0, convert the payment to the present value, and estimate the net present value.

Here the interest is not given, we are going to find out the value of I. For every future worth, we will convert it back to its present worth, and the Net present value =0, then $2000 =100*(1/1+i)+100*(1/1+i)^2+100*(1/1+i)^3+2500*(1/1+i)^3

Selecting different values for IRR.

Guessing I=10%.

We use trial and error, assuming that i=10% and then substituting. In this case, the left-hand side is 2000, while the RHS, the right-hand side, is $2127.17, and the net present value is $127.17.

But we need The NPV to be zero. This is the case of i=10%.

I’m guessing I = 12%. For a second trial, we will change the value of I; try i=12%. The net present value is $6.325; we are approaching the zero value.

Guessing I=12.4%..Try i=12.4%. After substituting. The net present value is $0.937.

Use an Excel sheet to get the value of IRR.

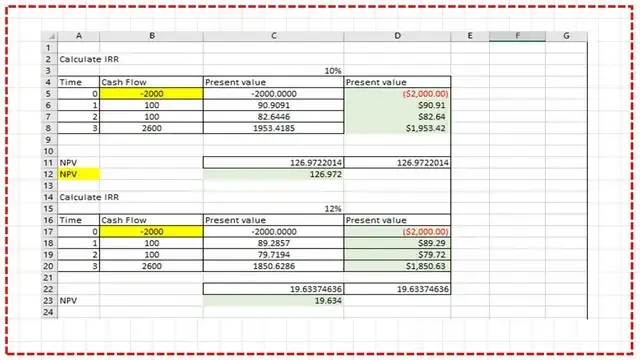
Now, we open an Excel sheet in tabulated form and check the steps we have done. First, in the first column, we put the value of Time as 0,1,2,3. In the second column, we list the values of the cash flow as shown in Excel. For the third year, we put the value of $2600.

For the present value equation, the value equals cash flow/(1+i). The value is = cell B5/(1+c3), first trial as 10%, as referential cell $C$3. Because we will repeat the value with common i, first estimate the c5=B5/(1+$c$3) A5, then make control+D.

The present value at the cash flow, for instance, when the cash flow =$100, at time =1 year.

The present value=100/(1.10)^1=$90.901, when the cash flow =$100 at time =2 year, the present value=100/(1.10)^1=$82.6446 and etc.

 We can use the Excel-built function and directly estimate the I; there is a function called the Pv, present value. We use the negative sign to get the required value; the present value =- Pv ($C$3, A5,0, B5,0).

The first item is I value $c$3. The second item, A5, is Time in Years. The third item is B5, which is the cash flow value for the year.

The fourth item is 0. The PV function gives—$2000 for cell D5 and $90.91 at D6. Open one bracket (interest, the year,0, cash flow,0). The same values are shown in column D from row 5 to row 8, the value of sum for C11=D11.

For the Present Net Value, we get the sum from time 0 to Time = 3, and the NPV =126.39772. We solved our previous problem by setting i=10%, then i=12%, then 12.40%, for which we obtained $-0.938.

For the IRR directly, we made trial and error to get a closer value to the IRR and then check the value that approaches zero.

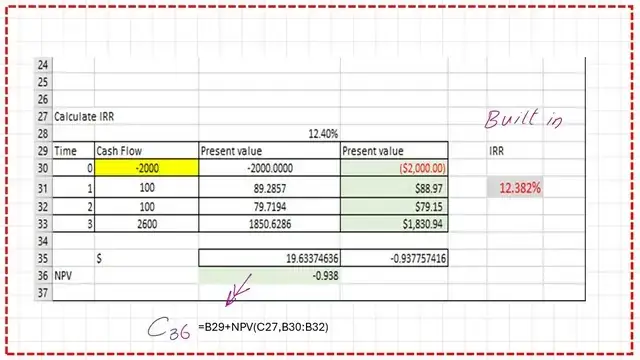
Use the built-in function in Excel to get the value of IRR.

We use the function IRR at cell F31, as F31=IRR (B30: B33) directly gives the value of the internal rate of Return as i=12.3816%; then, we get the internal rate of Return.

For the next posts: 8A-What is Capital Recovery?
This is a link to post 5 -Step-by-step illustration of solved problems for P-F value.

For a useful external resource, Engineering Economy, here is a link: Applying Theory to Practice.