Last Updated on December 26, 2025 by Maged kamel
We will solve practice problem 7-35, which involves developing load function W(x), shear function V(x), and moment function M(x) using the discontinuity function. The same problem is P 7-59 in the third edition.
- Part 1 of Practice problem-7-35 Discontinuity Functions.
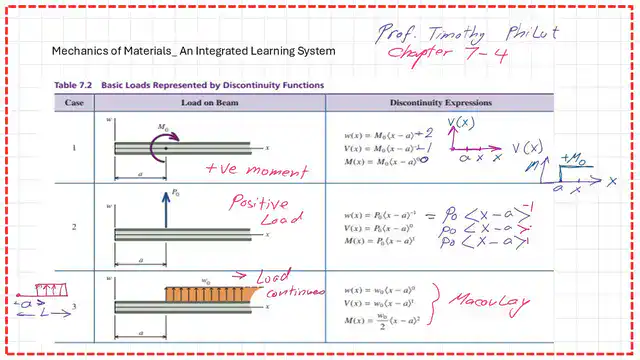
- What is the case in the discontinuity table that covers our Practice problem 7-35?
- Find the beam reactions for Part 1 of Practice problem-7-35.
- Write the three expressions for w(x), V(x), and M(x).
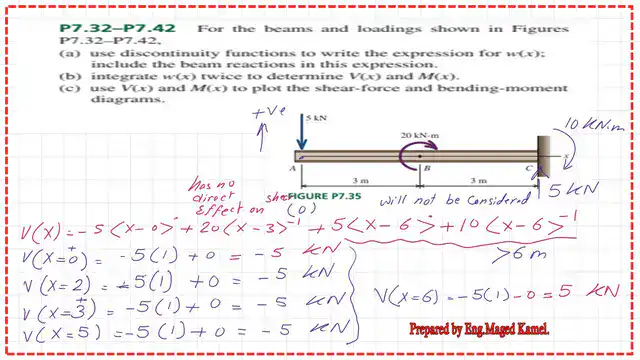
- The expression for V(x) over the range x = 0 to x = 5 m.
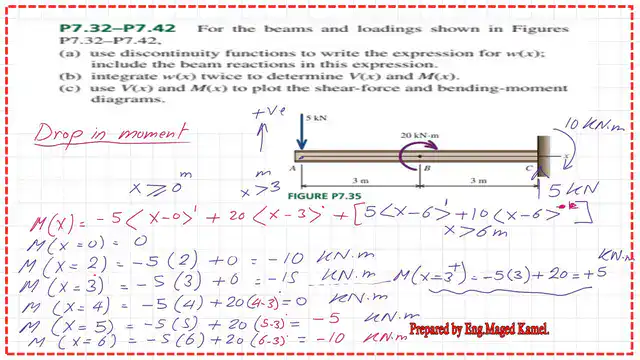
- Values for the expression for M(x) for x=0 to x=6m.
Part 1 of Practice problem-7-35 Discontinuity Functions.
This is part 1 of Practice problem-7-35. In this section, we will explore the various methods for solving it.
Understanding part 1 of Practice problem-7-35 is crucial for mastering the concepts involved.
The practice problem is included in Prof. Timothy Philpot’s book An Integrated Learning System, Mechanics of Materials. The same practice problem is on pages 7-56 in the third edition.
In part 1 of Practice problem-7-35, we will focus on deriving the shear and moment equations.
Part 1 of Practice problem-7-35 requires detailed attention to the application of equilibrium equations.
We have a given cantilever beam with a span of 6 m acted upon by one downward concentrated load of 5 KN at point A and one concentrated moment of 20 KN · m acting clockwise.
Part a) requires using the discontinuity function to write the expression for load w(x) in part a) and to include the beam reaction in the expression.
To solve part 1 of Practice problem-7-35, it is essential to analyze the load conditions thoroughly.
The results derived in part 1 of Practice problem-7-35 will guide the subsequent calculations.
In part b), w(x) must be integrated twice to determine the V(x) and M(x).
In part c), V(x) and M(x) must be used to plot shear force and bending moment diagrams.
Part 1 of Practice problem-7-35 is foundational for understanding the whole problem.
What is the case in the discontinuity table that covers our Practice problem 7-35?
In the next slide image, we can find the first and the second cases, where the beam is acted upon by a vertical load and a moment, covering our practice problem 7-35
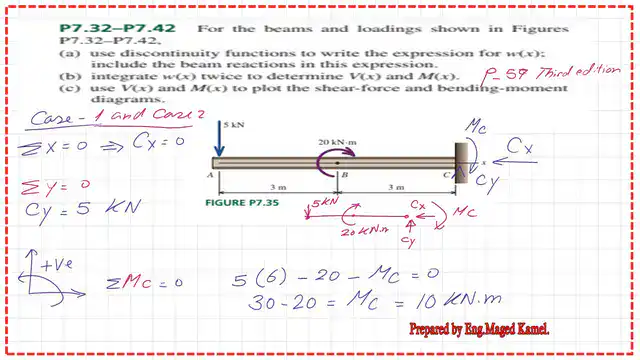
Find the beam reactions for Part 1 of Practice problem-7-35.
First, we draw the free-body diagram for the beam, which includes two reaction forces and a moment at the fixed support C: Cx, Cy, and Mc.
We are using the three equations of equilibrium: ∑X=0, ∑Y=0, and ∑M=0.
Following the standard rule for directions. For horizontal loads, the positive direction is to the right. For vertical loads, the positive direction is upward. For the moment, the positive direction is anticlockwise.
The horizontal reaction component is at Cx = 0 since there are no acting horizontal loads.
From ∑ Y=0, Cy =5 KN acting upward. From ∑M=0. Take a moment to consider all forces about the right support C, multiplying each force and reaction by the arm length to support D, and considering the directions of moment rotations. +5*6-20-Mc=0.
From ∑M=0. Take a moment to consider all forces about the right support C, multiplying each force and reaction by the arm length to support D, and considering the directions of moment rotations. +5*6-20-Mc=0. Mc value equals 10 KN · m; since it is positive, it means that it is in the assumed direction.
Write the three expressions for w(x), V(x), and M(x).
In the next slide, we are ready to write the expression for W(x) for the given beam; these are cases 1 & 2 from the discontinuity table discussed earlier. Consider the left point A as your 0,0 point. The horizontal axis X passes through the (0, 0) point. The Y-axis will be pointing upwards.
Following the positive direction, the upward direction for positive loads is essential. The Load of 5 KN Ay is downward, so it is negative, acting at x = 0. Therefore, we write -5*<x-0>^-1, as we are dealing with load intensity.
After three meters, there is a clockwise moment of 20 KN · m, so the expression is +20*<x-3>^-2. At x=6m, there is an Upward reaction load of 5 KN, its expression is +5*<x-6>^-1, and a moment of 20 KN · m, its expression is +0<x-3>^-1.
Finally, we have Cy of +5 KN acting at x = 6 m and a moment of +10 KN · m. The W(x)=-5*<x-0>^-1+20*<x-3>^-2+5<x-6>^-1+10*<x-6>^-2.
We do not consider the last two reactions in our calculation since they represent a step function for distances>6 m, as we will see next.
The next step is to integrate one to obtain V(x) for shear.
V(x)=-5*<x-0>^0+20*<x-3>^-1+5<x-6>^0+10*<x-6>^-1. We have integrated by adding only n+1, and we do not have divisions by n+1. Again integrate to get the value of M(x)=-5*<x-0>^1+20*<x-3>^0+5<x-6>^01+10*<x-6>^0. Then, parts A and B were completed.

The expression for V(x) over the range x = 0 to x = 5 m.
In the next slide, we write the expression for V(x) =-5*<x-0>^0+20*<x-3>^-1+5<x-6>^0+10*<x-6>^-1.
If x <3 the term *<x-3>^-1 is zero. If x>3, it will be positive.
The term <x-6>^0, if x is less than 6, is zero, while if x >6, the term is positive. The moment term does not affect shear. For x=0, V(0)=-5*1+0+0+0=-5 KN. For x=2, V(2)=-5*1+0+0+0=-5 KN. For x=3,
V(3)=-5*1+0+0+0=-5 KN. For x=4, V(4)=-5*1+0+0+0=-5 KN. For x=5, V(5)=-5*1+0+0+0=-5 KN.
For x=6, V(6)=-5*1+0+0+0=-5 KN.
Values for the expression for M(x) for x=0 to x=6m.
In the next slide, we write the expression for M(x). M(x)=-5*<x-0>^1+20*<x-3>^0+5<x-6>^01+10*<x-6>^0. For x=0, M(x=0 )=-5*(0)=0 KN.M.
For x=2 M, M(x=2)=-5*(2-0)^1=-10 KN.M. For x=3 M, M(x=3)=-5*(3-0)^1=-15 KN.M.
This summary concludes part 1 of Practice problem-7-35, reinforcing key concepts.
Make sure to revisit part 1 of Practice problem-7-35 for any clarifications.
For x=3 plus M(x=3 plus)=-5*(3-0)^1+20*(+ve)^0=-15+20=+5 KN.M.
For x=4 M, M(x=4)=-5*(4-0)^1+20*(+ve)^0=-20+20= 0 KN.M.
For x=5 M, M(x=5)=-5*(5-0)^1+20*(5-3)^0=-25+20=-5 KN.M.
For x=6 M, M(x=6)=-5*(6-0)^1+20*(6-3)^0=-30+20=-10 KN.M.
This is the end of Part 1 of Practice problem-7-35 Discontinuity Functions.
Please refer to the second part of this post, in which we will use Excel expressions to draw both the shear and moment diagrams.
The previous post is the 3a-Part 2 of Practice problem-7-32 Discontinuity Functions.
A video is associated with this post; the link is provided below.
This is an introductory link to Macaulay’s function on Wikipedia.
DEFLECTION – Macaulay’s Method (Double Integration) – Made Easy! (Strength Of Materials Series – Module #2 Book 1)-Amazon.
The PDf for the data of this post can be downloaded.