Last Updated on March 21, 2024 by Maged kamel

How To Compute Critical Stress-Table 4-22?

Critical stress by Table 4-22.

Our subject as of today will be how to estimate critical stress -Table 4-22. The controlling factor, that differentiates between short columns and long columns is the criteria, of Kl/r, we evaluate the maximum value whether, in the x or y direction, we find that the maximum kL/r value will give the minimum compressive strength value.

Accordingly, we can evaluate the value in LRFD or ASD, How to use the tables to get the same result as evaluated by calculations, keep in mind that we are still on the subject of general buckling. We are going to use a solved problem.

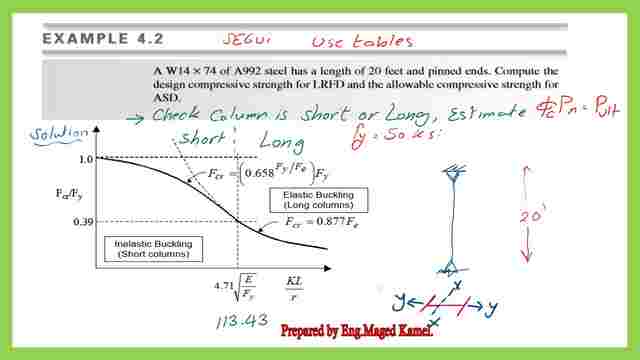
The same solved problem explained earlier in the previous post, which was solved problem 4-2, was including W14x74 of A992 steel, the height was 20 feet and the column was hinged from both ends, computing the design compressive strength by LRFD and ASD. let us refer back to our graph as shown in the next image with Part of Table 4-22.

How to compute critical stress-table 4-22?

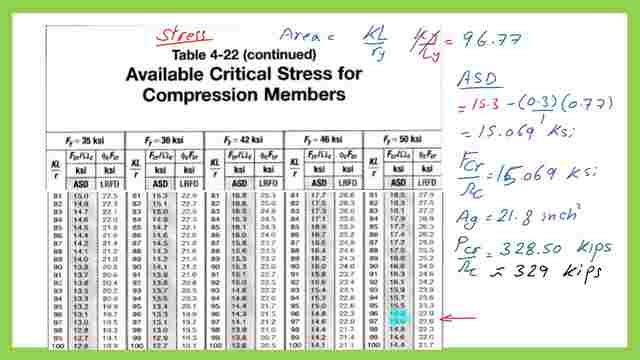
Table 4-22 is a table that gives the value of available critical stress for various values of yield stress, Fy from 35 ksi till Fy is 50 ksi. The table assumes that the governing (KL/r) is in the y-direction as being the bigger value as compared with the value of (KL/r)x in the x-direction.

But sometimes, we have several braces for a column, that let the column has several buckling curves about the major axis that could lead to a lower value of (KL/r).

We use a fake value of (KL/r) for the buckling in the major axis and convert this value to the corresponding to Kl/r in the y-direction to compare this fake value with the actual (K*L/r) in the minor axis, then select the maximum value to use in table 4-22.

This is a solved problem 4.2 that includes a column of  W14x74 of A992 steel, the height was 20 feet and the column was hinged from both ends. It is required to compute the design compressive strength by LRFD and ASD.part of the content of our post.

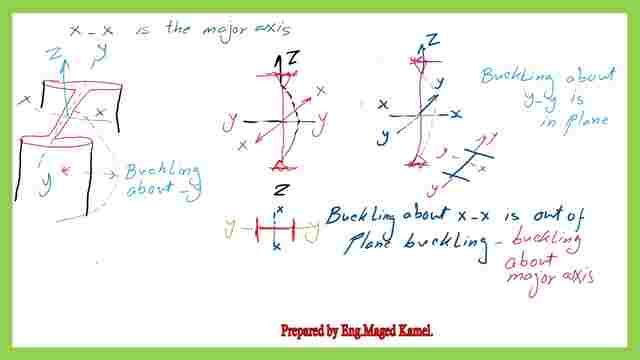
To imagine the shape of buckling in the x-direction, assume you are pressing in the middle of the column in the y-direction, perpendicular in the direction of x, if we want to imagine the buckling in the y-direction, press at the middle of the column, in the x-direction out of plane buckling as shown in the oriented shape. The difference between buckling about a major axis and buckling about the minor axis-in plane and out of a plane.

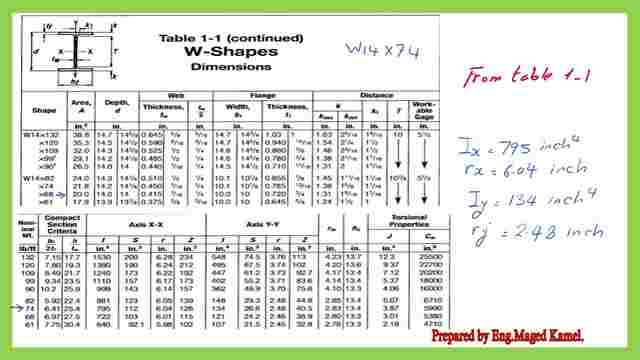
1-Use table 1-1 to get the necessary information for the given section.

The major items to continue estimating the critical stress is to find the values for rx,ry, Ix, Iy. The next slide image shows the detailed data for the given w 14×74 column.

2-How to covert kx*lx to equivalent ky*Ly?

In our case, where kx*Lx is = ky*Ly, we convert kx*lx to equivalent ky*ly, since, the tables for the compressive strength evaluation are based on ky*ly /ry,  he has converted the kx *Lx into equivalent ky* ly.

Since we are looking for the max=( kx* Lx ,ky Ly ), that is ky *Ly which in our case is =20, so the controlling factor, is the y-direction used in the design is ky *ly/ry =20*12/2.48 = 96.77, we use this value in the table.

The division of rx/ry=6.04/ 2.48. the buckling in the x-direction it is =8.21 is < ky* ly=20.

3-Compute critical stress-table 4-22 for LRFD design load.

We are going to use Table 4-22, since our Fy =50 ksi,  first for LRFD, our k *L / r in y which is =96.77, from Fy =50 ksi, for the k*l/r =96.77 it is in between 96 and 97, for LRFD, for 96 the value is 22.9. While for 97 the value is 22.6, so our value will be < 22.9 and estimated as =22.9 minus the difference between (22.9-22.6) * 0.77/ 1, which will give the value of 22.67 ksi, we will multiply by the area to get the load for the LRFD =494.18 kips.

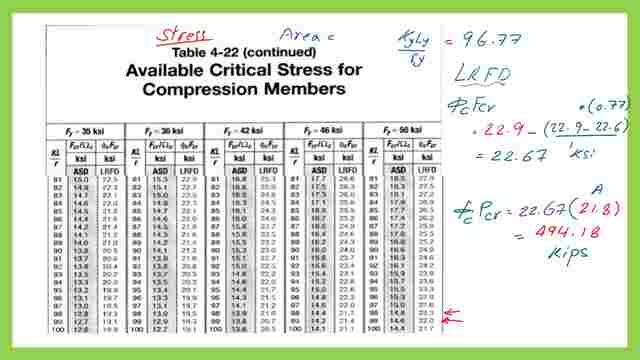
4-Compute critical stress-table 4-22 for ASD design load.

This is Table 4-22 we are checking the critical stress based on the ASD design. For ASD, for K*L/r= 96, (1/Ω)*Fcr= 15.30 ksi, while for K*L/r= 97, (1/Ω)*Fcr= 15.0 ksi. So (1/Ω)*Fcr for 96.77is <15.30 ksi and estimated as (15.30 –(15.30-15.00)* (0.30/1)=15.069  ksi, we will *A, to get the load for the ASD: (1/Ω)*Pcr =329 kips.          

  In this solved problem, we considered the equivalent of k_x *L_x /rx,  how to convert to the equivalent value of ky ly, and how to use table 4-22, maybe the idea will be cleared, in other examples, where the control of bracing is performed to make the k_x *L_x /r_x is the controlling factor.

This is the pdf file used in the illustration of this post.

If you wish to review the Column Compressive strength by the general provision
This is the next post, A Solved Problem 4-9 For available compressive strength.
For a good external reference for the compression members.