Last Updated on June 7, 2024 by Maged kamel
- A Solved problem-8-34 for a nominal uniform load.
- Nominal uniform load for the first span by the lower bound method.
- Nominal uniform load for the second span by the lower bound method.
- Solved problem-8-34-Plastic nominal uniform load Wn for the first span by the upper bound theorem.
- Wn for the second span by the upper bound theorem-solved problem-8-34.
- Nominal uniform load for the first span using MASTAN 2.
A Solved problem-8-34 for a nominal uniform load.
A solved problem-8-34, we have a continuous beam with three spans, the first span length=24′ and the second span length=36′, while the last span length=24′, the beam has a distributed uniform loading, the section of the beam is W27x84, Fy=50 KSI. The plastic modulus Zx= 244 inch3. it is required to estimate the nominal load for the beams that can develop plastic hinges and collapse load.
We need to find the indeterminacy number for the beams; we do not consider the horizontal loads. We have six unknowns, two moments, and four vertical unknown loads. Based on the summation of Y and moment equals zero. We will deduct 2. The indeterminacy number is equal to 6-2=4.
We have 7 hinges to be placed at spans AC, CD, and DE. The number of mechanisms is equal to 7-4 = 3.
From the given W27x84, we can find the Zx value and estimate the plastic moment, equal to 50* 244 = 12200 inches. Kips. The final value of Mp is equal to 1016.66 ft. kips.
We can get the plastic moment value by multiplying 50*244 and the result is 12200 inch. kips, to convert it to foot kips, divide by 12. The Mp value will be equal to 1016.66 Ft. kips. This value is the value in the third span due to symmetry.
The three possible mechanisms for the three beams are shown in the next slide. Each mechanism is created from three plastic hinges.
Nominal uniform load for the first span by the lower bound method.
We can estimate the plastic moment for the first span by equating the moment from reactions and uniform load with the plastic moment at the middle of the first span. The Wn value obtained using the lower bound method equals 28.24 kips/ft. Please refer to the next slide image for more details.
Nominal uniform load for the second span by the lower bound method.
For the second span, we can get the value of Wn that creates three plastic hinges, two at the support and one at the mid-span. Again, we equate the moment from the reaction at the left support with the moment from the uniform load to Mp.
The value of Wn is estimated to be 12.551 ft/kips.
We will use the Upper bound theory to get the values of Wn for both the first and second spans.
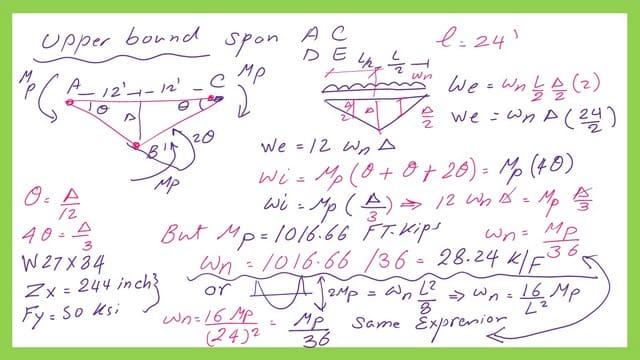
Solved problem-8-34-Plastic nominal uniform load Wn for the first span by the upper bound theorem.
to get the plastic moment from the upper bound theorem, we will equate the external work by the uniform wn to the internal work due to the plastic moments. We will estimate end slopes in terms of delta.
The slope of each side due to the deflection delta Δ, θ= tan θ=Δ/12. The external work= internal work, the external work=Wn*(0.50*Δ*24)=12*Wn*Δ. We have three MP due to the three hinges. The internal work=Mp*θ+Mp*θ+Mp*(θ+θ).
The internal work=Mp*θ*412*Wn*Δ=Mp*θ*4=Mp*4*Δ/12. Δ goes with Δ.Wn=1*Mp/36.
The plastic moment value is known, equal to 1016.66 ft. kips; we can get the Wn value as Wn=1Mp/36. = 1016.66/36 = 28.24 kips/ft. the same result can be obtained by considering that 2Mp equals Wn*L^2/8.
Wn for the second span by the upper bound theorem-solved problem-8-34.
Due to symmetry, the deflection is Δ at the mid-span.The slope at each angle=Δ/18. The external work= = internal work. Wn*36*(0.50*Δ)=18*Wn*Δ.
The internal work equals 4Mp*θ, but theta θ =tan θ=Δ/18, and the internal work=2*Mp*Δ/9. The Wn can be estimated and its value is equal to 12.55 Ft. kips. The same value of Wn can be verified by equation wnl^2/8 to two mp. Please refer to the next slide image.
We will examine all the possible values of the nominal loads from the different mechanisms and select the lowest value of Wn, which is Wn=12.55 kips/ft.

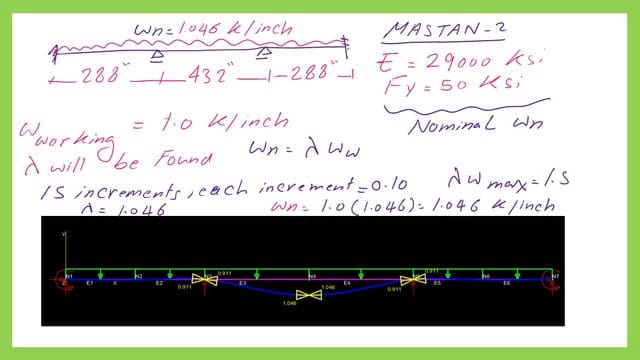
Nominal uniform load for the first span using MASTAN 2.
We can use MASTAN 2, the first inelastic analysis, to get the value for Wn, the nominal uniform load. The modulus of Elasticity for steel E considered is equal to 29000 ksi, and Fy=50 ksi. These two parameters are necessary to find the plastic nominal uniform load. The beam lengths are to be converted to inches.
The working load is to be in kips/inch, and I have considered a working load of 1.00 kips/inch. There are 15 increments, each 0.10.
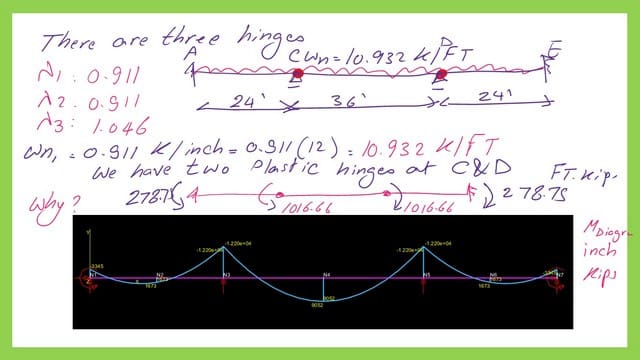
According to the next slide, three plastic hinges have been developed. The first hinge is located between the two supports, and one is at the midpoint of the second span. Wn has a value of 1.046 kip/ inch, which matches our Wn in kips/ft after the conversation.
Two plastic hinges were created at a lower value of Wn equal to 10.932 Kips /ft or 0.911 kips/inch
.With the help of MASTAN 2, we can find the moment values for the three beams, please refer to the next slide image for more information.
The shear value for beams due to the nominal load can also be estimated based on the program. The sum of vertical forces and reactions is equal to zero. Please refer to the calculations attached herewith. Thank You all.
Have more information about the structural analysis –III.
For the next post, 38-solved problem 10-1-Design of steel section for continuous beam part-1/3.