Solved problem 8-22-Plastic nominal load.
In the first solved problem 8-22, we use the given section of ASTM A992 and plastic theory. Determine the value of the P-nominal and W-nominal as indicated. We have several examples for M nominal, including concentrated loads P loads, and others, containing uniformly distributed loads, W nominal to be estimated. This example is from Prof. McCormick’s chapter 8. We have Fy=50 ksi and Zx value is 153 inch3 from CM#15, page 1-19.


Solved problem 8-22-Plastic nominal load by using the lower bound theorem.
The first method is the lower-bound theory. or the statical method, in which, we check the number of indeterminacy and then convert the system to an unstable system, we have three reactions at A and 3 reactions at B the total number is 6, to get the degree of indeterminacy.
We have three reactions, horizontal, vertical, and moment, and the same at the other support B. The number of indeterminacy=3+3-3=3 degrees of indeterminacy.
We will covert the system to Statically determinate, we need to add some hinges=6-3=3. For the three hinges, one hinge is at A, the second one is at B, and the third one is at C, since no horizontal load, the system needs 3 hinges only to be unstable.
We need to estimate the M positive and the M negative and lay the two diagrams together then check the maximum positive M plastic value since the collapse will occur at the maximum value of M plastic. For the beam shown, we estimate the reactions at A and B, RA=Pc12/32, Rb=Pc20/32, Mc=RA20’=Pc2012/32=240 *Pc/32, this is the moment as a function of Pn.


The next step is to include Mp negative at support A. Mp negative at the other support B, and drop the value of M-positive.
The hatched triangle below the datum represents the M=ve value, for which the maximum value is the Mp value.


Solved problem 8-22-Plastic nominal load by the upper bound theorem.
In the next slide, this is the Upper bound, with the mechanism with an assumed hinge location under the load, there is a slope of θ value at the left and θ1 at the right support.
If we consider the deflection at C=Δ, θ=tan θ=Δ/20, θ1=tan θ1=Δ/12.
We have Mp, which is a positive plastic moment with an angle=θ+θ1, and two plastic moments at the two supports, at support A, for which the angle is θ, while at support B, the angle is θ1.
The internal Work =Mp*θ+Mp*θ1+Mp*(θ+θ1). For θ+θ1=(Δ/20)+(Δ/12)=32*Δ/240.
The external work Pn*Δ=Mp*(2*θ+2*θ1)=2*Mp*(θ+θ1)=2*Mp*(32*Δ/240, Delta Δ goes with Δ, Pn=Mp*(64/240).
Pn=(8/30)*Mp, since Mp=Mn=637.50 Ft.kips.
The plastic nominal load Pn=170.0 kips, which is the same result as the value obtained from the lower bound method


Solved problem 8-22-Plastic nominal load by MASTAN 2.
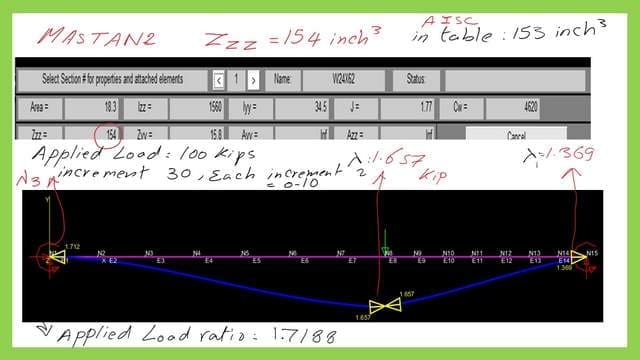
I have used MASTAN 2 first inelastic analysis to find the plastic nominal load for the given beam. One observation is that the plastic section modulus considered for the W section is 154 inch3 instead of 153 inch3 which will create a small change in the results. I have created nodes in inches and connected these nodes by elements and the material is steel with E 29000 ksi and Fy =50 ksi.
locations of the plastic hinges and the lambda values.
The applied load I used P0 is 100 kips. I have made 30 increments with the value of 0.10, so the total load after 30 increments will be three times the initial load P0.
As we can see from the next slide image we have three plastic Hinges with different lambda values. The first plastic hinge, it will be created at the right support with a lambda value of 1.369 which means that applying (1.369*100=136.9 kips) will create a plastic moment of (154*50=7700 inch. kips.

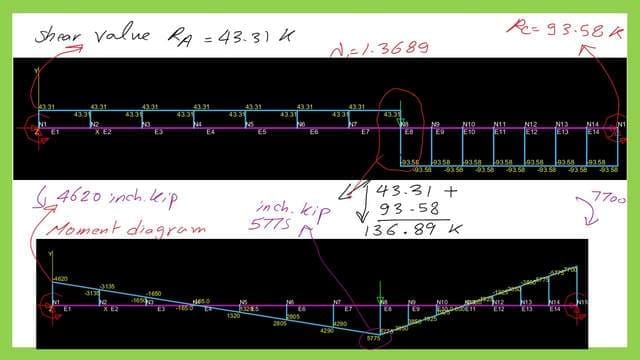
The first plastic hinge and the values of the moments.
For the first plastic hinge, the beam is acted upon by P=136.89 kips and has two moments, the first moment is at support A equals 4620 inches. kips and the moment at support c which equals the Plastic moment value of 7700 inch. kips.
The value of Ma and Mb is less than 7700 inch. kips, which is why no plastic hinges will be created.


We can see that program MASTAN 2 can give the shear diagram and bending moment for each increment and we can see these values for the load equals 136.89 kips.

The second plastic hinge and the values of the moments.
For the second plastic hinge, the beam is acted upon by P=165.73 kips and has two moments, the first moment is at support A equals 6403 inch. kips and the moment at support c which equals the Plastic moment value of 7700 inch.kips.
Due to the increased value of the load we can see that Mb will be equal to 7700 inch. kips and the second plastic hinge is formed..


The third plastic hinge and the values of the moments.
For the third plastic hinge, the beam is acted upon by P=171.18 kips and has two moments, the first moment is at support A equals 7700 inch. kips and the moment at support c which equals the Plastic moment value of 7700 inch. kips. Due to the increased value of the load we have three hinges for the beam.


Thanks a lot and hope to see you in the next post.
This is the pdf file used in the illustration of this post but without the added data for MASTAN 2.
Have more information about the structural analysis –III.
For the next post, Solved problems 8-32 for the plastic Nominal Uniform load.

