Last Updated on February 21, 2026 by Maged kamel
Review of Shear Stresses for Steel Beams.
The following slide shows the topics we will discuss in this post.
Introduction to shear stress for beams and proof that both vertical and horizontal shear stresses are equal.
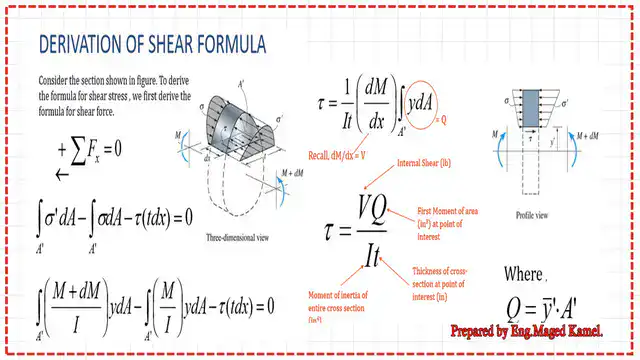
If we take two sections of a beam apart by a distance, at elevation y, there will be two compression forces due to the two values of M and M + dM, resulting from the moment difference.
The stress, calculated from the known formula f = M*y/I, will be multiplied by dA, resulting in two compressive forces. These forces are not equal because of the current difference in the moment, which equals dM. To create a balance, a shear force acting horizontally will be created.
As the sum of Fx =0, the shear force is developed to create a balance; this force value equals shear stress* area=τ*dx*b=σ’*dA-σ*dA, but (σ’-σ)*dA (dM)*y/Ix, then τ*dx*t=dM*y/I.
How do we derive the expression for shear stress?
Making integration, we get an expression for the stress for shear τ=∫dMy*dA/(dx*t)=V*Q/I*T, where V is the shear.
Q is the first moment of the area at the point of interest, I is the moment of inertia for the section, and finally,t is the breadth of the section. Please refer to the following slide image for more details.
Horizontal shear stress for beams.
For the balance of a beam element, the horizontal stress of shear should be accompanied by vertical stress due to shear, as shown in the next slide.
It is proven that the value of τh=τv, where τv is the vertical stress due to shear, while τh is the horizontal stress due to shear, by multiplying by area and taking a moment at the edge.
The PDF containing the data for this post can be viewed or downloaded from the following link.
This is a link to the next post, ‘A Solved Problem for Shear Stress.’
The following post will contain a solved problem for stress estimation for different shapes.
For more detailed shear in bending, please read the link: Shear in Bending. This links to Boston University’s Mechanical Engineering.
Here is the link to Chapter 8, “Bending Members.” A Beginner’s Guide to the Steel Construction Manual, 14th ed. Section 8.3.1 Shear Behavior.
Here is the link to Chapter 8, “Bending Members.” A Beginner’s Guide to the Steel Construction Manual, 15th ed. Section 8.3.1 Shear Behavior.
Here is the link to Chapter 8, “Bending Members.” A Beginner’s Guide to the Steel Construction Manual, 16th ed. Section 8.3.1 Shear Behavior.