Last Updated on April 29, 2024 by Maged kamel

Solved problem 3-8-1 for staggered Bolts.

In this post, we’ll discuss fastener load transfer and its relationship to net area estimation. The approach used in the solved problem can be considered a refinement for determining the final net area.

We have a solved problem 3-8-1 for the staggered Bolt, introduced in Salmon’s textbook Steel Structures Fifth Edition.

Introduction to solved problem 3-8-1 for staggered Bolts.

Calculate the governing net area for plate A of the single lap joint in Fig. 3.8.1 and show free body diagrams of portions of plate A with sections through each line of holes assume that Plate b has an adequate net area and does not control the strength T.

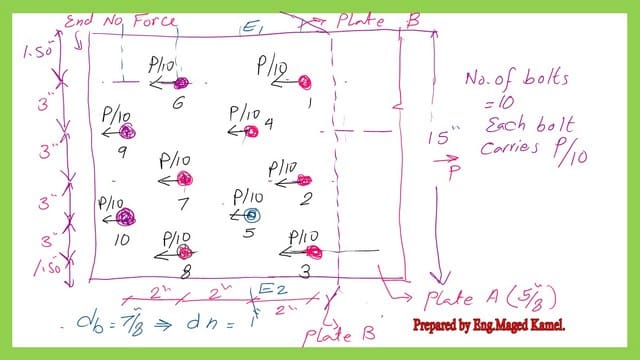
In the next image, there is a detailed plan for the arrangements of fasteners for plate A, which is under tension force P and has a thickness of 5/8 inches. Another plate B is on the back side of plate A and is connected with plate A using 10 bolts. Each bolt carries one-tenth of the load P.

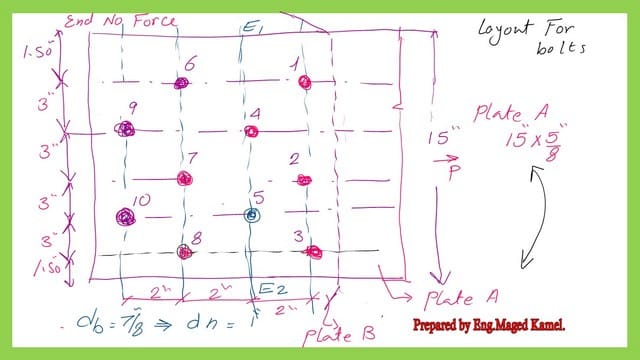
It is required to estimate the minimum net area for given plate A by considering the different routes and finding out the modified net area values under the effect of load transfer.

We add 1/8 inch to the diameter of each bolt to get the hole diameter, which will equal one inch.

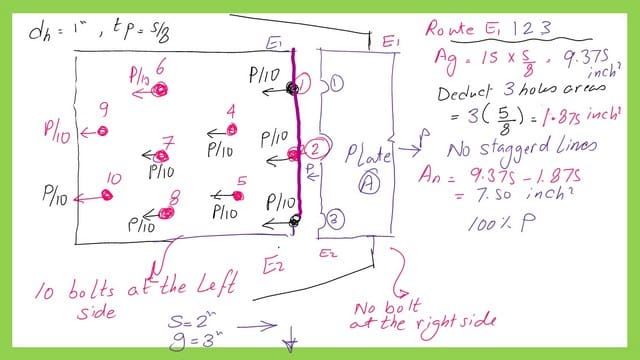
The net area for the first vertical route E-1-2-3-E2.

The first route E1-2-3-E is a vertical line through three bolts taken at the right side of these bolts. If we look at the section, There is a force P on the right side is balanced by the same value P. No bolts are located at the rightside of the section.

The gross area of Plate A is found to be equal to (159*5/8)=9.7375 inch2, the area of holes are 1.875 inch2. The net area of the route is 7.50 inch2, the section can carry 100% of the load.

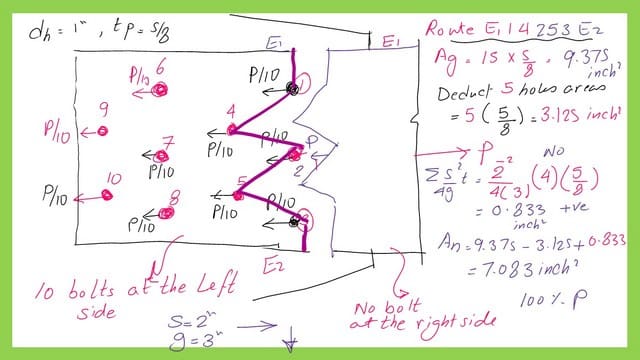
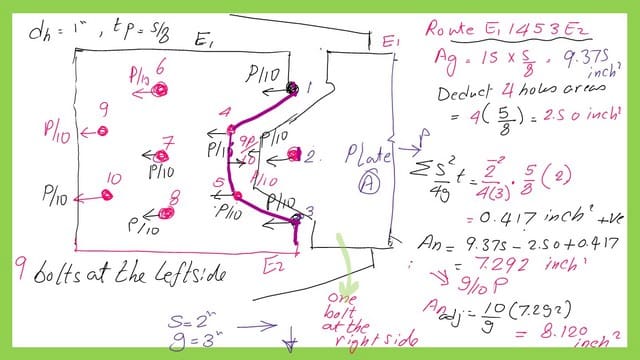
The net area for the second route is E1-4-2-5-3-E2 with staggered bolts.

The second route E1-4-2-5-3-E2 is another route, but it has three staggered lines 1-4, 4-2, 2-5 and 5-3. There is no bolts are the rightside of the route.

The gross area of Plate A is 9.7375 inch2, The route passes through five holes and the area of these holes to be deducted from the gross area to get the net area.The area of holes are 3.125 inch2. We use the sum of S^2/4g*tp to get the added areas for the route, where S is the distance between bolts and g is the vertical distance between bolts. the s value is 2 inches and g value is 3 inches.

The area added equals 0.833 inch2. the final net area equals (9.375-3.125+0.833 )=7.083 inch2.
No modification for the net area is to be done, since the section carries 100% P.

The net area for the third route E1-4-5-E2.

The third route E1-4-5-E2 is a vertical section passes by three bolts. We notice that at the rightside of the section there are three bolts each carry P/10 P of the load P.

For the left side of the section, we have 7 bolts, each bolt is carrying P/10 The net area equals 8.125 inch2. A modification is made to the net area since the section carries (7P/10). The modified net area value equals (10/7)*8.125=11.607 inch2.

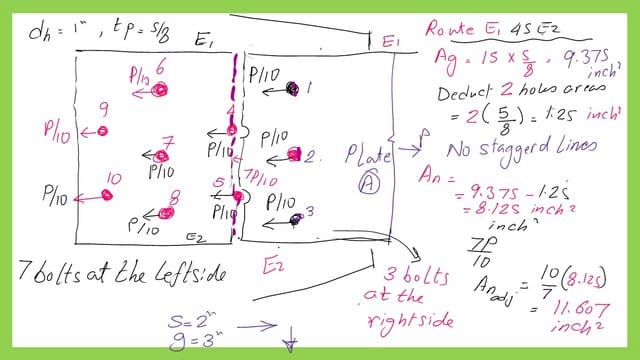
The net area for the fourth route E1-4-5-3-E2 with staggered bolts.

The fourth route E1-4-5-3-E2 is it has three staggered lines 1-4 and 5-3 . There is only one bolt at the rightside of the route.

At the left side of these bolts, there are 9 bolts. The net area will be found to be equal to 7.925 inch2. The modified net area due to load transfer is 8.12 inch2.

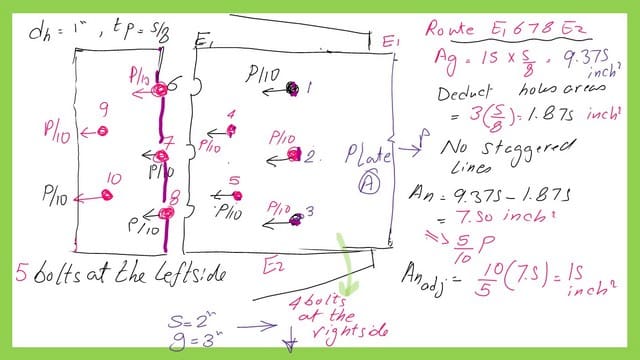
The net area for the fifth vertical route E1-6-7-8-E2 with no staggered bolts.

The fifth route E1-6-7-8-E2 is a vertical line through five bolts. There are five bolts at the right side. Again from the left side, we have also five bolts .

Net area will be found to be equal to 7.50 inch2. The modified net area due to load transfer is (7.50*10/2)=15.0 inch2. inch2.

What is the final net area for the section of plate A?

The table shows the different values of the net area for each route, we are concerned with the minimum value of the net areafor 100% P. As we can see, the lowest value of net area equals 7.083 inch2 for the section that carries 100% P. The section is route E1-1-4-2-5-2-E2. The full details are shown for each route and its net area.

The next post is Problem 3-4-3 for staggered bolts-tension members-1/2.-staggered bolts-1/2.
There is a very useful external link-Block Shear Rupture for a more detailed illustration of block shear. A Beginner’s Guide to the Steel Construction Manual, 14^th ed.