Last Updated on January 1, 2026 by Maged kamel
Full detailed illustration of the Moment of inertia Iy for a triangle.
Full detailed illustration of the Moment of inertia Iy for the triangle.
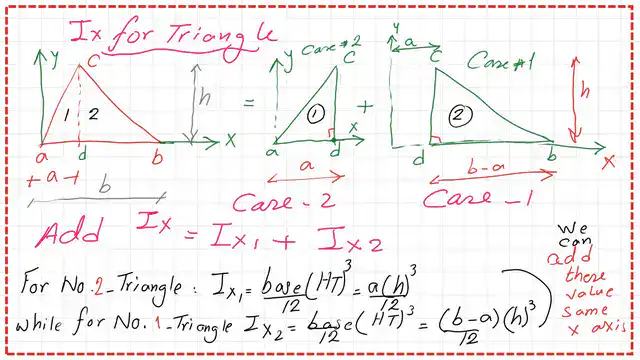
We aim to determine the moment of inertia Iy of the triangle about the y-axis through point a.
1-Since the triangle ABC consists of two triangles ACD and DBC, for the inertia of the triangle, we are going to add the sum of the two inertias for those two right angles about the same axis y.
2-The inertia for an angle adc about axis y passing by point a=Iy1=h*a^3/12, where a is the base of the triangle ADC, and h is the height.
Recall this value was estimated for the right-angle case no. 2. 3-The inertia for an angle dbc about axis y-dc passing by point d=Iy-dc=(b-a)^3*h/12/12, where b is the base of the triangle abc.
We have to estimate the inertia at the Cg for case 1 of the right-angle triangle, and from there, we can proceed to evaluate the inertia at any point.
4-For the second triangle dbc, we need to estimate Iy-CG, then we add (area*x bar^2), where the area is the area of the triangle dbc, x bar is the distance from its Cg to the Y axis.
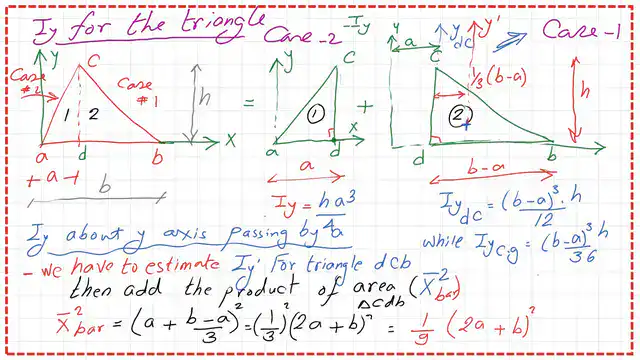
5- x bar distance as shown in the next slide, x bar=a+(b-a)1/3=(2/3)a+(b/3).
6- x^2-bar can be wriien asxbar^2=(1/9)*(2a+b)^2.
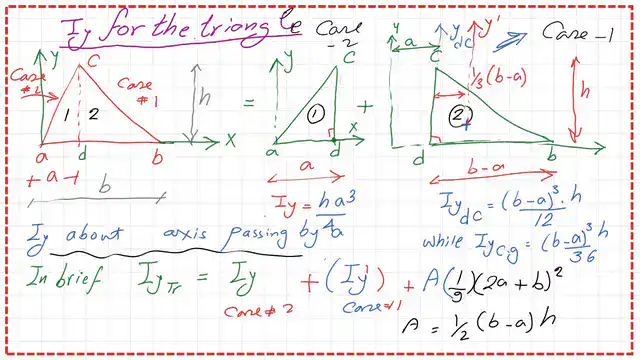
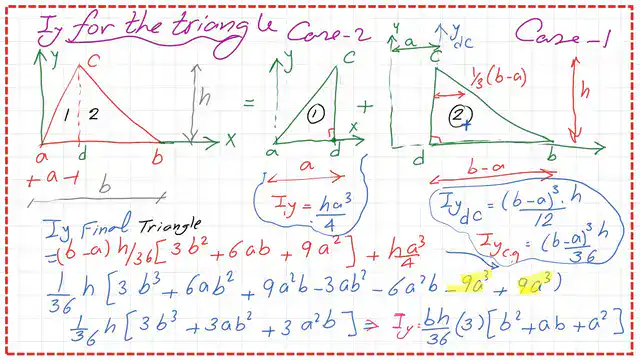
The final value of Iy-Iy final=Iy case -2 triangle+ Iy-cg for triangle dbc+A*x^2 bar.
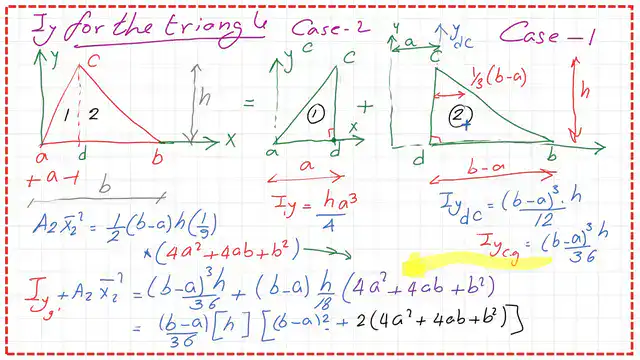
The following images show additional details of the summation process for Iy.
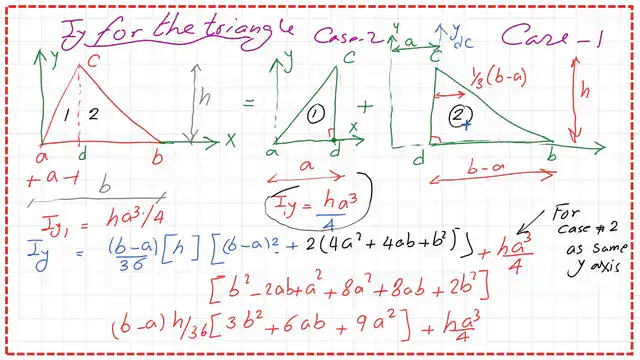
7-We substitute all the known values obtained earlier; the expression can be shown in the next slide image.
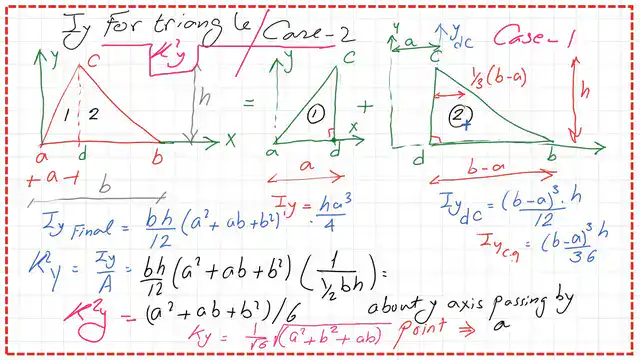
The radius of gyration for the triangle about the y-axis.
From the value of Iy by the area of the triangle, take the square root of the product, and then the value of ky can be found.
This is the final value of k^2y for the triangle.
We have completed the estimation of inertia Iy for a triangle, and we can check the result by comparing the inertia value with the NCEEs table.
This is the list of inertia for triangular shapes quoted from the NCEES tables of inertia.

You can download and review the content of this post and the next one through the following pdf file.
For an external resource, the definition of the moment of inertia with solved problems is the 2nd moment of inertia.
This is the next post, How to get of Moment of inertia Iy-at Cg for a triangle?