Last Updated on January 4, 2024 by Maged kamel

Solution of linear systems by LU-partial pivoting-1/2

In this post, we will discuss the solution Solution of linear systems by LU-partial pivot. Our aim is how to get x1,x2, and x3-using LU-partial pivot.

There is a solved problem in our post which is the same problem we solved in the previous post by using Gaussian-partial decomposition. To check the previous post click here.

The first method is L&U side-by-side.

We have partial pivoting since the first element of the A matrix a11=0. We will swap row -1 to row 2. The matrix will be called matrix A1. Again we will write the L0 matrix as a (1 0 0, 0 1 0, 0 0 1). For the L0 matrix, no swap will be considered.

To get the U1 matrix where the two elements below the pivot 4 will be set=0, we will multiply (0/4)*R1+R2, there will be no change in this second row but the value of new a21 will be =0. This multiplication factor is 0.

For the third row, we will multiply by (-2/4)*R1 and add it to R-3. The multiplication factor is (-1/2).

As for the lower matrix L1, we will change the sign of the previous multiplication factor and use(0, +1/2) as L21, and L31 respectively.

L1 matrix is ( (1 0 0, 0 1 0, +1/2 0 1) .

We will proceed to the second pivot, (Row 2/ column2) which is +2, we will select the absolute maximum value for the elements below the second pivot. We have one element which is 5.5. The swap will be made between row 2 and row 3.

The lower matrix L1 will have a swap between row 2 and row 3 it will be as a 3×3 matrix and will be arranged as (1 0 0, 1/2 1 0, 0 0 1).

We want to make element a32 value to be zero, then we will multiply a32 by(-2/5.50)*R2 and add to row 3. We will get the final U matrix arranged as (4 -3 2, 0 5.5-4, 0 0 4.4545).

The sign of the multiplication factor will be reversed for the lower matrix L2 and will be considered as (+2/5.50).

The final Value of L2 will be as (1 0 0, 1/2 1 0, 0 +2/5.50 1). L2 will be considered as the lower matrix L.

We use the equation PA=L*U, and P is the multiplication of P23*P12, which can be found as (0 1 0, 0 0 1, 1 0 0).

The P matrix will be multiplied by the original matrix A and will be compared with the multiplication of L*U. Both equations should have the same result. The full details of the PA values and The product of L by U is shown in detail in the next slide image.

The second method, Uses an elimination matrix and a permutation matrix.

The equation used in the solving of this problem will be P*A=L*U, where P is the permutation matrix. A is the coefficient matrix, L is the Lower matrix, and U is the upper matrix. We want to solve for the values of the three unkownsx1,x2, x3.

row1 to row2.

We write the coefficient matrix as a 3×3 matrix, please refer to the next slide image for more details. The first pivot is equal to 0. This is the case of partial pivoting. the absolute maximum value is 4. We will swap the first row and the second. Swapping means that we will multiply by P12, which stands for shifting row1- to row2.

we will rewrite the equation as P12*A=A1. A1 is the new matrix results from the shifting of row-1 to row-2.

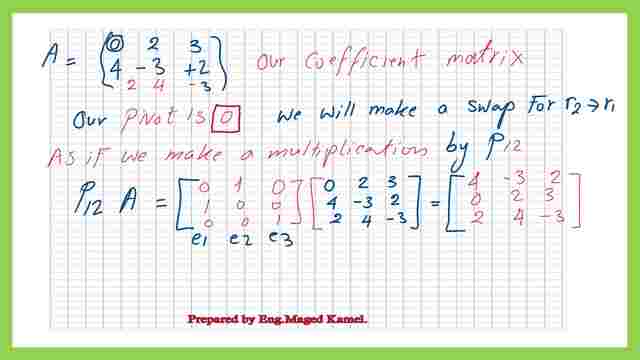
Create an elimination multiplication factor for a21.

We will multiply the third row by(-a31/a11) for the matrix A1. the product will be added to the third row. The element a31 value will be zero, we will have new values of a32 and a33. The matrix A1 will be changed and become a new matrix, which we will call A2.

We can write the elimination matrix M1, which is the elimination matrix with 3 rows and 3 columns. The third row /the first column is the multiplication factor (-a31/a11) which is equal to -2/4)=-1/2. The M1 diagonal is 1.

If we want to check that M1*P12*A=A2, we can write all three matrices and perform the multiplication process as we can see in the next slide image.

Create a permutation matrix P23.

We will check the second pivot of matrix A2, which is 2, and we will select the maximum value of the elements in the same column below that pivot. We have only one element, which is 5.50. We will create a new pivot by swapping row 2 to row 3. The swap can be expressed as a new multiplication by permutation matrix P23.

Equate P23*M1*P12*A to matrix A3.

We will rewrite the equation as P23*M1*P12*A and equate it to the new matrix which is matrix A3. Check the sequence of the operations we are moving from right to left for the operations.

Create an elimination multiplication factor for a32.

We will multiply the third row by(-a32/a22) for the matrix A3. The product will be added to the third row. The element a32 value will be zero, we will have new values of a33. The matrix A13 will be changed and become a new matrix, which we will call A4.

We can write the elimination matrix M2, which is the elimination matrix with 3 rows and 3 columns. The third row /the second column is the multiplication factor (-a33/a22) which is equal to (-2/5.5). The M2 diagonal is 1.

Equate M2*P23*M1*P12*A to matrix A4.

We will rewrite the equation as M2*P23*M1*P12*A and equate it to the new matrix which is matrix A4. Check the sequence of the operations we are moving from right to left for the operations.

Check matrix A4, we will find that this is the upper matrix that we are looking for. the details can be seen in the next slide image.

This is the end of part-1. We will continue in the next post for the solution of linear systems by LU-partial pivoting-2/2.

Link to Omni calculator-LU Decomposition Calculator.