Last Updated on March 21, 2024 by Maged kamel

Introduction to Crout’s LU decomposition for a 2×2 matrix.

The elements of the upper and lower matrix, 2×2, can be obtained by using the Gauss elimination method. Next is how to solve for x,y for two equations using the lower upper triangulation, through an example.

Step-1-derive the expression for Crout’s LU decomposition for a 2×2 matrix.

We have two equations for which we want to develop Crout’s LU decomposition for a 2×2 matrix. The first equation is (2x+3y=13) and the second equation is (3x+4y=18). As we can see the determinant of the matrix equals -1, not zero.

Then the matrix is invertible. We set this Matrix A to be equal to two matrices multiplied by each other One of these is called the lower Matrix. The other Matrix is the upper Matrix.

The lower Matrix is expressed as lij. Where I represent the row and j represents the column. The lower Matrix has L11, L22, and l21 in the case of 2×2 matrix nonzeros. The element L12 is zero. For the symbols, we will write A matrix (2 3 3 4); we are saying a11, a12, a21, and a22.

Unlike the previous method LU decomposition, Crout’s LU decomposition for the 2×2 matrix considers that the upper matrix has a diagonal=1, beside the lower corner element=U21=0, while The L matrix’s diagonal based on Crout’s LU decomposition for 2×2 matrix is not =1.

Step-2-The values for L and U matrices for Crout’s LU decomposition for a 2×2 matrix.

Since A = the lower multiplication by the upper matrices, we will perform the multiplication of lower and upper metrics and equate the product to the elements of matrix A. The multiplication of the  First row by the first column, we can express as L11=a11.

The multiplication of the  First row by the second column we can express as (L11*U12)=a12.If we multiply the second row by the first column, we can express it as  (L21)=a21.

If we multiply the second row by the second column, we can express it as  (L21*U12)+U22=a22. From equations I and III we have L11=a11&L21=a12. From equation II, we get U12=a12/a11. Finally,L22=a22-(a21*(a12/a11)).

We apply this information for the given matrix A which is (2  3  3 4). The first column will be placed as the first column of the L matrix.

We need to have the value of L22. For the U matrix, we have diagonals U11&U22=1, while U12=a12/a11=3/2.

Perform the row echelon to convert matrix A to an upper matrix, taking the value of U22 as the value of L22. The final value of L22=-1/2.

For the given two sets of equations, 2x + 3y = 13 and 3x + 4y = 18.We have A=(2 3 3 4), b=(13 18). Since A*x=b, while A=L*U. Consider U*x=c. Then L*c=b. Since L and b are known, we can get the value of C, but we need to estimate the inverse of matrix L.

The other alternative is to multiply U-1*L-1*x and equate the value to b. Then X=U-1L-1b.

Step-3-Derive the value for the inverse matrix L-1 for Crout’s LU decomposition for a 2×2 matrix.

We will get the inverse matrix L-1, for a 2×2 matrix, we can get the determinant swap the corner element, and change the signs for the other diagonal. The determinant value of L=-1.The inverse matrix of L is (1/2 0 3 -2). We will make a check that L*l-1=I.

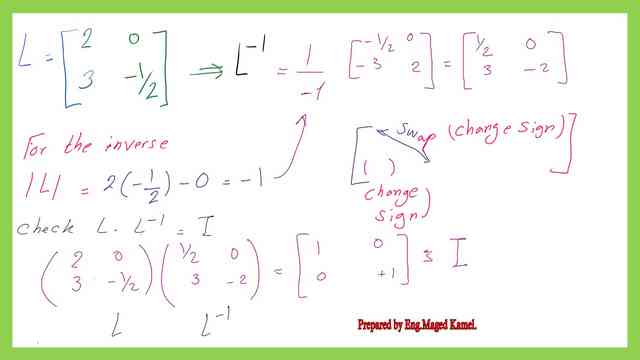
Step-4-get the values for the C matrix for Crout’s LU decomposition for a 2×2 matrix.

We can estimate the value of matrix C by multiplying L-1*B, L-1 we have just estimated, while b matrix is (2×1) matrix= ( 13 18). As we can see C=(13/2 3), is a 2×1 matrix. Since Ux= C, we can get the value of the unknowns by multiplying U-1*C.

Step 5-get the values inverse matrix U-1 for Crout’s LU decomposition for a 2×2 matrix.

We can get the inverse of matrix U, by using the identity matrix, the inverse of Matrix U is a 2×2 matrix with elements as ( 1  -3/2  0  1). Multiply U-1*C to get the X vector. The inverse of Matrix U is a 2×2 matrix with elements as ( 1 -3/2 0 1). We can get X=2 and y=3.

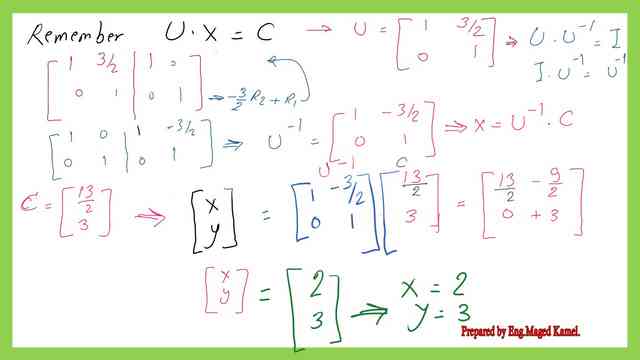
Step 6-get the values for x, and y from matrix C for Crout’s LU decomposition for a 2×2 matrix.

The final value of X – the matrix can be estimated as a (2×1) matrix, 2 3). We will check our given equation to satisfy the requirements. As an alternative method to estimate the vector-matrix X, multiply U-1L-1B. The calculation will yield the same values for x and Y.

This is the pdf file used for the illustration of this post.

The next post: Crout’s LU decomposition for a 3×3 matrix.

This is the Omni calculator for estimating various items of linear algebra -LU Decomposition Calculator.

This is a link to another –Calculator for matrices.