Two Solved Problems For Economic Equivalence.
Solved problem For Economic Equivalence.
A solved problem 1.3 is from Prof. Anthony Tarquin’s book, basics of Engineering Economy.
The following solved problem For Economic Equivalence is a good example of Equivalence, for the different 5 statements need to be checked whether the right or wrong.
Problem 1.3- AC-Delco makes auto batteries available to General Motors dealers through a privately owned distributorship.
In general, batteries are stored throughout the year



A 5% cost increase is added each year to cover the inventory carrying charges for the distributorship owner. Assume you own the City Center Delco facility.
Make the calculations necessary to show which of the following statements are true and which are false about battery costs.
a. The amount of $98 now is equivalent to a cost of $105.60 one year from now.
b. A truck battery cost of $200 one year ago is equivalent to $205 now.
c. A $38 cost now is equivalent to $39.90 one year from now.
d. A $3000 cost now is equivalent to $2887.14 one year ago.
e. The carrying charge accumulated in 1 year on an investment of $2000 worth of batteries is $100.
The solution for the solved problem of Economic equivalence for all the different statements is as follows:
1-The first option for economic equivalence of $98 to $105.60 with a rate of 5 % is a false statement, since 98*(1.05)=$102.90, which is the value after one year, does not=$105.60.
2-The second option for equivalence of $200 of truck battery cost one year ago is not equivalent to $205.0 now, with a rate of 5 %. The statement is false since 200*(1.05)=$210 does not=$205.0.
3-The third option for equivalence of $38 cost now is not equivalent to $39.90 one year from Now, with a rate of 5 %The statement is false, since 38*(1.05)=$39.90.
4-The fourth option for equivalence of $3000 cost now is not equivalent to $2887.14 one year ago, with a rate of 5 %. The statement is false since 3000/(1.05)=$2857.14 does not=$2887.14.
5-The fifth option for equivalence of $2000 carrying charge of $100, with a rate of 5 %. The statement is true since 2000*0.05=$100.
Economic equivalence is an important principle that is used as a means of comparing alternatives.



The second Solved problem of the two solved problems for economic equivalence.
If we have several alternatives, the method of comparison between them is by choosing a time period and finding the value for the present time or the present value of the flows.
A solved problem is quoted from Contemporary Engineering Economics 6th Edition by Chan Park (Author). It is not included in the video.
let us suppose that an electronics manufacturing company buys a machine for $25000 and borrows $20000 from a bank at a 9% annual interest. In addition, the company pays a $200 loan origination fee when the loan commences.


The bank offers two plans as follows: plan 1– P=$20,000 with interest is 9% plus a $200 fee at the first year and in equal installments of $5141.85 from year 1 to year 5 with a total number of five.
The second plan–Plan 2 is to pay $200, loan fee, at time=0, and in equal installments of $1800, the total numbers are 4, starting from time t=1 and the final payment at time t=5. Both plans have the same timetable of 5 years and the same interest rate of 9% yearly. The next table 3.1 shows the details of each plan.
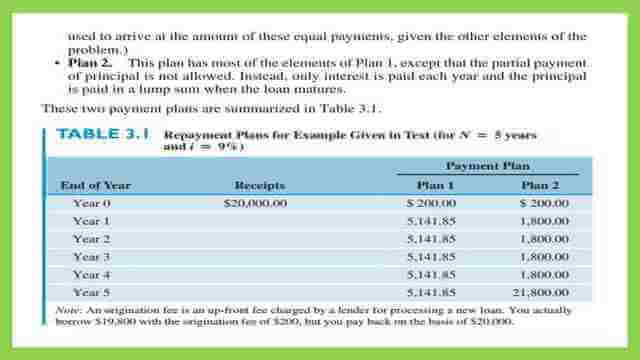

How could we compare the two plans? Is the comparison based on the total amount of payments? for instance, for plan 1 the total amount of payment will be =200+5141.85*5=$25,909, while for plan 2 the total amount of payment =200+1800*4+21,800=$29,200. The criteria of comparison between the two plans are to use the economic equivalence, both plans have the same time=5 years and the same interest of 9%.


By converting each payment into its future value at time 5, and comparing these future values of the two plans, we can select then the appropriate plan. Here is the cash flow diagram for both plans.
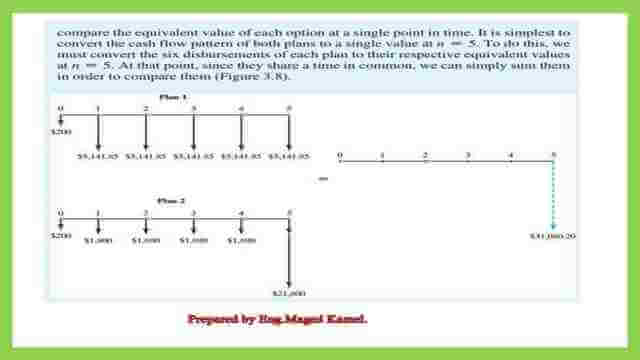

Detailed calculations of plan 1.
This is the detailed calculations for plan-1, pay $200 at time=0, and equal installments of $5,141.85 the total numbers are 5, starting from time t=1. We add all the future values for these payments. We get $31,080.


Detailed calculations of plan 2.
These are the detailed calculations for plan 2 pay $200 at time=0, and equal installments of $1,800 the total numbers are 5, starting from time t=1. We add all the future values for these payments. We get $31,080.


This is the complete calculation for plan 2. Comparing the future worth value of both plans we will find that they have the same F5 value, future value at the end of the fifth year, hence these plans are economically equivalent to each other. The borrower can then select the appropriate plan that suits him.
This is the pdf file used in the illustration of this post.
The next post title is Simple Interest and Compound Interest Part -1.
Engineering Economy Applying Theory to Practice is a good reference.


