Last Updated on January 8, 2024 by Maged kamel
How to Use a matrix for the quadratic function?
In two posts, we discussed the quadratic function or the quadratic interpolation function. The first post is an easy introduction to quadratic interpolation, and the second post is Solved problems for quadratic interpolation.
In this post, we will solve three problems, and the main idea of these solved problems is to use the matrix for the quadratic function to get the values of its parameters or simply get the quadratic matrix.
The first solved problem for the matrix for the quadratic function
Using the row-echelon form-interpolating polynomial function.
As a practice problem, use a matrix for the quadratic function. It is required to find the interpolating polynomial function P(t)=a0+a1t+a2t^2 for the given data points which are (1,12),(2,15), and (3,16).
We start by writing the three equations for P(t) for the given three points as follows:
We plug in the value of t=1, and P(1) equals 12. The first equation is P(1)=a0+a1(1)+a2(1)^2=12. We plug in the value of t=2, and P(1) equals 15. The second equation is P(2)=a0+a1(2)+a2(2)^2=15. We plug in the value of t=3, and P(1) equals 16. The second equation is P(3)=a0+a1(3)+a2(3)^2=16.
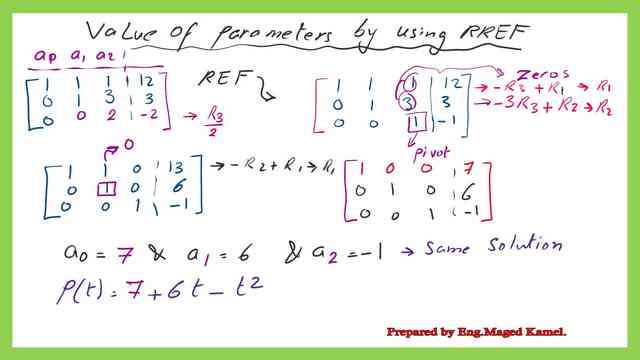
Our Unknowns are a0 & a1 and a2. By using the augmented matrix; we will find the first row as (1 1 1 12). The second row is (1 2 4 15). Finally, the last row is (1 3 9 16). We will convert the augmented matrix to the row echelon form.

The first row has a leading item equal to 1; to let a21 and a32 equal zero, we will perform the elementary row operations as we can see in the next slide image. Multiply the first row by -1 and add the value to the second row, while for the third row, we will multiply the first row by minus one and add the value to the third row.
Next, we will move to the second leading item in the second row, equal to 1; we will let the element a22 equal to zero by multiplying the second row by -2 and adding the value to the third row. As we can see, we have the row echelon form for the quadratic function. We have a0=7. We can use back substitution to get the value of a1 and a2.

Use a reduced row echelon form-interpolating polynomial function.
If we wish to use the reduced row echelon form, for the matrix for the quadratic function, we want to have zeros above the pivots for the third and second rows. We consider a33 as a pivot, then multiply R2*-3 and add the value to R2; we will get a zero for the element a23. We will multiply the third row by -1 and add the value to the first row.
Next, we will move to the second pivot column. Multiply R2*-1 and add the value to R4; we will get a zero for element a12. We have a0=7& a1=6, and a2=-1. We can rewrite the interpolating polynomial as P(t)=1+6*t-t^2.
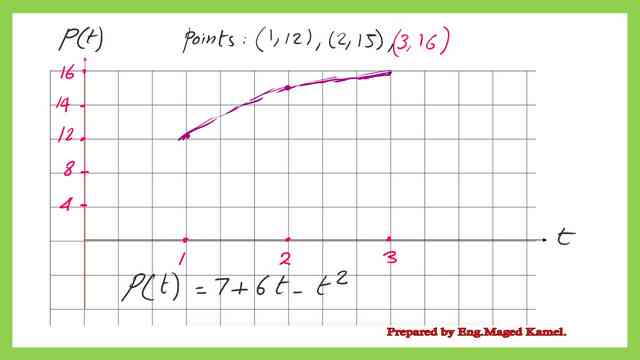
Check the interpolating function for the given three points’ data. The details can be seen in the next slide image.

This is a graph for the interpolating Quadratic polynomial.
The second solved problem for the matrix for the quadratic polynomial function.
The second solved problem is a practice problem, for the matrix for the quadratic function. It is required to find the quadratic polynomial function P(t)=a0+a1x+a2x^2 that satisfies the condition P(0)=f(0), p'(0)=f'(0) and p”(0)=f”(0).
In this solved problem, instead of giving three points. One point is given, and the slope at that point shall be equal to the slope of the original function, which is e^2x. The second derivative P”(0) is equal also to the second derivation of the original function, which is e^2x.
The interpolating quadratic polynomial y value at point zero is estimated by plugging in the function e^2x and setting x=0; the value at point zero equals e^0=1.
The first and second derivatives of the original function are estimated at x=0, as shown in the next slide image. We start by writing the three equations for P(x) for the given data: We plug in the value of x=0, and P(0) equals 1. The expression is P(x)=ax^2+bx+c. The first equation is P(0)=a(0)^2+b(0)+C=1. We plug in the value of P'(0), equal to 2. The expression is P'(x)=2ax+b. The second equation is P'(0)=2a(0)+b=2.
We plug in the value of P”(0), equal to 4. The expression is P”(x)=2a. The third equation is P”(0)=2a=4. We can write the three equations in the form of two-matrix multiplication. The product is equal to (1 2 4).

We can write the augmented matrix. We will swap the first and third rows in the row echelon form. We can convert the row echelon form to a reduced echelon form. The final values for a,b, and c can be obtained as a=2,b=2, and c=1. The polynomial can be written as p(x)=2x^2+2x+1.
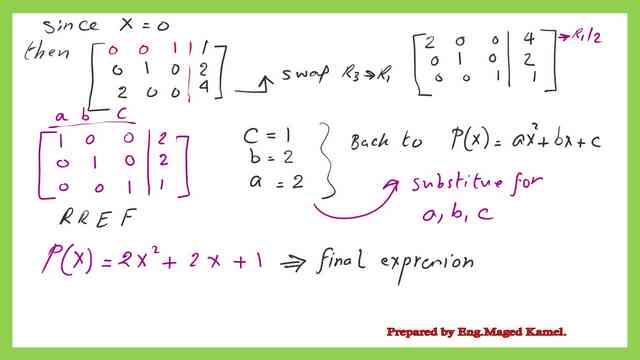
The third solved problem for the matrix for the quadratic function.
For the third solved problem for a quadratic matrix.It is required to find the quadratic polynomial function P(t)=a0+a1x+a2x^2 that satisfies the condition P(1)=f(1),p'(1)=f'(1) and p”(1)=f”(1).
One point is given, and the slope at that point shall be equal to the slope of the original function, which is xe^(x-1). The second derivative P”(0) is equal also to the second derivation of the original function, which is xe^(x-1). The interpolating quadratic polynomial y value at point zero is estimated by plugging in the function xe^(x-1) and setting x=1; the value at point zero equals 1*e^(1-1)=1.
The first and second derivatives of the original function are estimated at x=1. Estimating the first and second derivative values is shown in the next slide image.

We start by writing the three equations for P(x) for the given data: We plug in the value of x=1, and P(1) equals 1. The expression is P(x)=ax^2+bx+c.The first equation is P(1)=a(1)^2+b(1)+C=1. We plug in the value of P'(1), equal to 2. The expression is P'(x)=2ax+b. The second equation is P'(1)=2a(1)+b=2. We plug in the value of P”(1), equal to 3. The expression is P”(x)=2a. The third equation is P”(1)=2a=3.
We can write the augmented matrix. We will swap the first and third rows in the row echelon form. We have a row echelon form for the third solved problem. We will convert it to the reduced echelon form.

We can write the augmented matrix. We will swap the first and third rows in the row echelon form. We can convert the row echelon form to a reduced echelon form. The final values for a,b, and c can be obtained as a=3/2, b=-1, and c=1/2. The final value for the polynomial is shown in the next slide image.

For a useful external link, math is fun for the matrix part.

