Last Updated on February 22, 2026 by Maged kamel
Introduction to structural loads-LRFD and ASD.
Content of the post.
We’ll discuss the dead load and live load, and the associated tables with the allowed live load and dead load values. The environmental loads are to be included as well .Next, we’ll learn how to create a load combination.
Two approaches will be employed. The first will use the LRFD coefficients. LRFD stands for load factor resistance design.
In this design strategy, we shall simultaneously increase the dead loads and live loads. We are going to lessen the element’s strength. As we shall see later, strength reduction factors will depend on the kinds of acting forces and moments.
The acceptable strength design is shortened to ASD. This design approach is a variation of the working stress or factor of safety. To determine the allowed stress in that working design method, the yield stress was multiplied by a safety factor.
Thus, the working stress design approach, or WSDM, has been modified.
Dead load is a structural load.
Table 17-12 on this slide contains the usual material densities we use to determine the dead load value. We also offer cast and hammered aluminum, which weighs between 159 and 171 pounds per square foot.
Different materials exist, such as lead, copper, and iron. Our steel deck includes a manufacturer’s comment.
The stone is structurally lightweight and suspended; its weight is given in lb/sq ft.
Other items, like partitions and drywall partitions, contain studs and sheets.
There is a wall category, whether it is made of brick or CMU block. The 4-inch CMU blocks weigh 29 lb/square ft. The different finishes category is also given, such as Terrazzo 1 inch weight 13 lb/ft2.
Live load as a structural load.
The next table source is ASCE-02. The title is the minimum uniformly distributed live loads, L0, and the minimum concentrated live loads. The Access floor system office’s uniform loads are estimated at 50 lb/ft2. The corresponding KN/m2 is 50.0.
For the assembly areas and theaters, fixed seats are fastened to the floor. The uniform weight in lb/ft2 is 60.00. The corresponding weight in KN/m2 is 2.87. For balconies (exterior). The uniform lb/ft2 is 100.00. The Si units’ corresponding uniform load is 4.79 KN/m2. For corridors, the uniform load is 100 lb/ft2.
We continue checking table-4-1. For hospitals, the operating room weight, as a uniform load, is 60lb/ft2, equivalent to 2.87 kN/m2. Private rooms have a uniform load of 40 lb/ft2, equivalent to 1.92 KN/m2. For Office building live loads, file and computer rooms shall be designed based on anticipated occupancy. For Lobbies, the uniform load is 100 lb/ft2, equivalent to 4.97 kN/m2.
Introduction to LRFD design
The next subject is Load and Resistance Factor Design (LRFD). LRFD is a method for designing structures so that no applicable limit state is exceeded when a structure is subjected to all appropriate combinations of factored loads. A limit state is a condition in which a structure becomes unfit.
Structural members can have several limit states. Strength limits state concerns about safety and relates to the maximum load-carrying capacity (e.g., Plastic hinge and buckling).
Serviceability limit states related to performance under normal service load (e.g., excessive Deformation and vibration). The formula may summarize the LRFD method as applied to each limit state.
Σγi Qi <=φRn. γi are factors that are multiplied by loads. Qs are loads, whether dead load, live loads, wind, earthquake, etc. Φ is a reduction factor for the strength. While the R strength capacity of the member. Φ is a reduction factor for the strength. While the R strength capacity of the member. The ultimate loads should be less than or equal to the modified strength.
Types of structural loads and related symbols.
In the next slide, we will check the types of loads and symbols. We start with the dead load, denoted D. The next load is the live load, denoted L, which includes the gravity load due to intended usage and occupancy, including the weight of people, furniture, movable equipment, and partitions.
In LRFD, the notation L refers to floor live loads, and Lr refers to live roof loads. R. denotes rain loads. The snow loads are indicated by S.E., which denotes earthquake loads. W represents wind loads.
Environmental loads.
What are the environmental loads? Environmental loads are loads due to the environment.
Snow. In colder states, snow loads are often significant. One inch of snow is equivalent to a load of approximately 0.5 PSF. But it may be higher at lower elevations when snow is denser. For roof designs, snow loads ranging from 10 to 40 psf are commonly used. Snow loads are increased due to poor drainage systems, leading to accumulation.
Rain as an environmental Load.
The second environmental load is Rain. Though snow loads are a more severe problem than rain loads for the usual roof, the situation may be reversed for flat roofs, particularly those in warmer climates. if water on a flat roof accumulates faster than it runs off, the result is ponding or accumulation of rainwater. Ponding causes the roof to deflect into a dish shape that can hold more water.
Wind as an environmental Load.
The third environmental load is the wind load. A survey of engineering literature over the past 150 years shows a greater number of references to wind-induced structural failures. The most infamous of these have been bridge failures, such as those of the Tay Bridge in Scotland in 1879, which caused the death of 75 persons.
Earthquake as an Environmental Load.
For earthquake loads, seismic forces must be considered in the design of all types of structures.
Another definition for the limit state.
Another definition of the limit state is a condition in which a structure or part of a structure ceases to perform its intended function. Strength limit stats define load-carrying capacity, including excessive yielding, buckling, fatigue, and gross body motion. Serviceability Limits state the acceptable limits of fine performance, including deflection, cracking, slipping, vibration, and deterioration. All limit states must be prevented.
LRFD load parameters.
We will start by discussing the parameters of γi. The first formula is 1.4D. This formula is applied when there is only a dead load. No other loads exist during construction, which is the case.
For dead and live loads in a structure, the formula is 1.2D + 1.6L, plus the load acting on the roof: 0.50(Lr, snow, or rain). The biggest value is shown. The third formula is (1.2D + 1.6 (Lr or S or R) + (0.5L or 0.80W).
The loads considered are D& w&L&Lr and roof loads. The higher value of 0.50 L or 0.80 W should be considered. In the fourth formula, the wind direction is in the direction of the Dead load. The formula includes 1.2D + 1.3W + 0.5L + 0.5 (lr or S or R).
The earthquake is acting in the direction of the Dead load. We have 1.2D+-1.0E+0.5L+0.2S; plus if the E is in the direction of D, and minus if the E is opposite D.
The abbreviations for all the loads used in the different combinations are on the right-hand side.
Symbols are γ load factor,φ resistance factor, and Ω safety factor.
D & L&W are not necessarily loads only; they could also be shear forces or moments applied to a structure.
Torsional moments may also apply. For instance, if a given moment due to a dead load case is given, plus a moment due to a live load is given, then 1.2D+1.6L means multiplying the dead moment value by 1.20 and the live load Moment by 1.60.
Sometimes the shear is given as Ql, the live load shear force acting.
For the live load case, multiply by 1.60. Sometimes, factored dead is given, meaning the load is already multiplied by the load factor.
This is explained in the next slide. Note that D, L, W, S, etc. Loads are, in a general sense, those that include bending moment, shear, axial force, and torsional moment. Sometimes, these internal forces are called load effects.
Thus, the symbol D means dead load, load moment, load shear, and axial force. For a moment, we estimate the ultimate moments as 1.2Md + 1.6Ml. The previous load factors, 1.4D + 1.7L, can be found in earlier versions of the books.
LRFD Resistance Factors
The reduction factor Φ is not a constant; it varies depending on the condition of load, tension members, compression members, beams under flexure, and fasteners. Φ=0.90 is used for tension members (yielding state), and Φ=0.75 is used for tension members (fracture state).Φ=0.90 is used for compression members.
ASD load parameters.
For the ASD Design method, the loads D, L, W, and E are not multiplied by the load factor. For the strength factor, instead of multiplying by Φ, the design is divided by Ω, which is the safety factor, as shown. The first formula is ΣγQ=D. The second formula is ΣγQ=D+L+H.
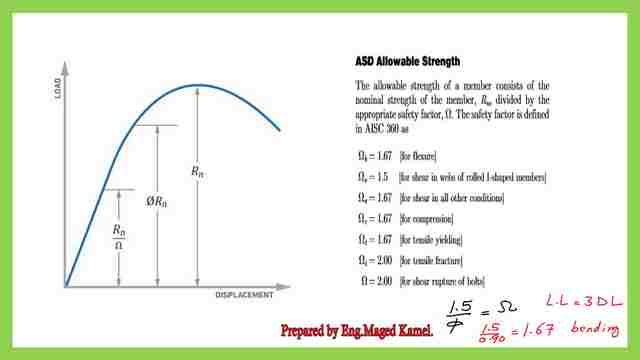
The third formula is ΣγQ = D + (Lr or S or R) + H. The fourth formula is ΣγQ = D + 0.75L + H + 0.75 (Lr or S or R). If we plot the relationship between displacement and load, the nominal strength is Rn.
In the case of LRFD, we multiply by φ to have φ*Rn. In the case of ASD, we divide by Ω, which is 1.67 for the moment. The value of Ω is shown on the slide: Ω = 1.67 for compression. Ω =1.67 in the case of tensile yielding.
The initial slope of the curve is a straight line from zero to the yield stress. The ASD value =Rn/Ω.The relation between the Ω value and Φ is 1.50/Φ=Ω. If we have Φ = 0.90 in bending, 1.50/0.9 = 1.67 is the bending reduction factor in the ASD design if the Live load equals 3 times the Dead Load value.
If you want to see the major changes between CM #14 and CM#15 regarding the different grades of steel and their uses for steel elements and bars, please refer to post 1A.
The PDF for this post can be reviewed or downloaded from the following documents.
In the next post, we will solve an example using the different load factors for LRFD and ASD designs.
This is a link to a very good reference, Chapter 1 – Introduction–An Overview of the AISC Steel Construction Manual, 14th Edition
This is a link to a very good reference, Chapter 1 – Introduction–An Overview of the AISC Steel Construction Manual, 15th Edition
This is a link to a very good reference, Chapter 1 – Introduction–An Overview of the AISC Steel Construction Manual, 16th Edition.