Last Updated on March 21, 2024 by Maged kamel

Study of Local Buckling-Part-2.

Local Buckling-part-2-Dealing with the stiffened portion.

In local buckling-part-2. I Quote From Prof. Salmon’s book if we look at the stiffened plate shown, the picture which is on the left side. If we want to estimate the forces, these stresses that act is of maximum values at the edges and have a slight decrease towards the center.

If we want to estimate the average stress of-f-max, we will find can be represented by f-max with a portion of the section as if the Pn can be estimated as web thickness t to be multiplied by (be), that is the effective width, which is a part of the web, that carries the f-max multiplied by the product of (tw*be). The nominal load value Pn=tbefmax, then we can draw a new shape reduced section of the web, which we call an effective area, with height= b and width of tw acted upon by fmax .

Local Buckling-part-2-Dealing with the un-stiffened portion.

The stress distribution for the unstiffened part is shown on the right picture side.
As for the unstiffened part, we have stress f-max at the attached portion-stiffened- and stress of- f value at the free edge, then the distribution, in this case, can be considered as fav, the average stress over the entire area of the flange.

The nominal load, in this case, will be estimated as Pn of the flanges, being as unstiffened Pn=(tf*bf)* fav. the product of (bf*tf) will be considered as A gr or Gross area.

While for the unstiffened equation for Pn=(fav)Agr, multiply by(fmax/f max), then take (fav/fmax) as equal to Q_s . Pn can be set = Q_s*fmax*Agr, but for the part of an unstiffened section.

Based on the first equation, stiffened part, with Pn=( t*be)*fmax. or the product of effective area by maximum stress, where Aef=(t*be).

We will multiply by ( Agr / Agr), then the equation is still valid but again consider Aeff/Agr =Q_A.

We want to estimate the Pn for the whole section. A compression member composed of both stiffened and unstiffened elements would be treated as unstiffened for establishing the stress fav.

Now Consider the whole section as reduced with A effective having stress of fav. Pn =fav Aeff, then multiply by (fmax/fmax), then multiply by (Ag/Ag). Using the expression of both Qa and Qs. The final expression will Pn=Qa*Qs(f max*A gross).

We can estimate the Qs, then work with the determine the Q_A then multiply by the( fmax*Agross)  to estimate the Pn, but the procedure will be commenced after proofing that the column is short.

Local Buckling-part-2-Modification of the equation used to estimate Fcr.

The formula for the critical stress for the short column will be modified, due to the case of local buckling as Fcr=QsQa(0.658 ^(Q fy/fe)Fy, the capital Q is equal to the product of (QsQa).

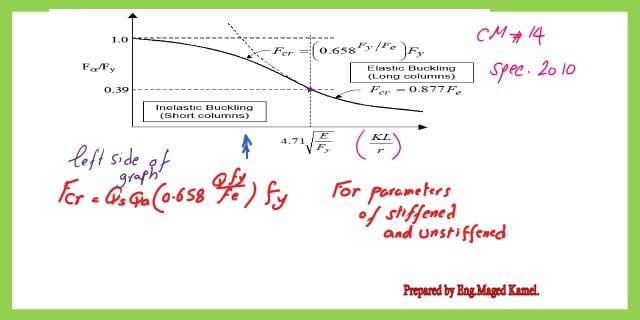
the Q factor is shown in the power for the equation as shown in the modified equation, these were for the parameters of stiffened and unstiffened sections.

Again we have to check the column is short or long by using the 4.71*sqrt(E/fy), if long column, we will use the equation for long columns, else use the equation for a short column.

limiting width-to-thickness ratios for un-stiffened sections.

Table B4.1a lists the values of width-to-thickness ratios for both unstiffened and stiffened shapes. There are four cases for the unstiffened parts; the First case is for rolled sections, the coefficient of bf/2tf of the flange is 0.56*sqrt(E/fy).

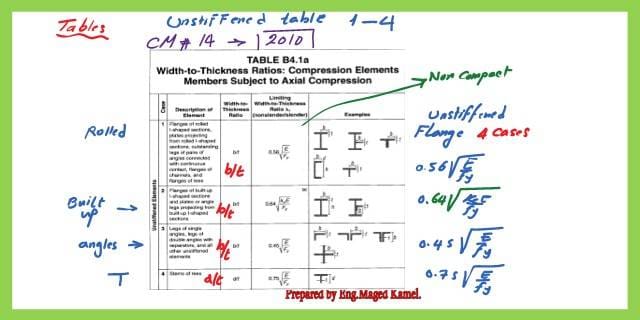
The second case is for the built-up sections or the portion protruding; the coefficient of the portion protruding, the coefficient of b/t is 0.64*sqrt(E/fy).

The third case is for the single or the double angle or intersection parts; the coefficient of b/t is 0.45*sqrt(E/fy).

For the T section, the fourth case, the coefficient of b/t is 0.75*sqrt(E/fy).

There are tables for both stiffened and unstiffened compression members, that is table B4.1A, based on AISC for unstiffened table 1-4 rev B is for the requirement for design there are 4 cases for the unstiffened the First case is for rolled sections.

limiting width-to-thickness ratios for stiffened sections.

The stiffened sections are from case no. 5 to case No.9 showing the coefficients for the W section, HSS, plates welded, all other stiffened elements, and round HSS.

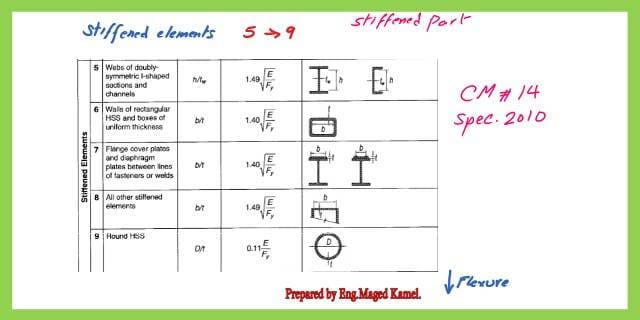
Case 5 -h/tw is the case of doubly symmetric, the limiting width to thickness is 1.49*sqrt(E/fy)

For local buckling-part-2. While inspecting case 6, we will find that this section’s parts are all stiffened, as has a section.

For case, no.7 b/t the limiting width to thickness is 1.40*sqrt(E/fy).

For Case no.8 all other stiffened elements, b/t the limiting width to thickness is 1.49*sqrt(E/fy).

The last case is the case of round HSS where D/t is the width-to-thickness ratio, the limiting width to thickness 0.11*sqrt(E/fy).

This is the pdf file used in the illustration of this post and the previous post.

The next post is 11- Local Buckling for stiffened and un-stiffened elements.
For an external resource, Concentrically Loaded Compression Members.