Last Updated on February 29, 2024 by Maged kamel
Introduction to the moment of inertia.
A summary of the different types of inertia.
There is the area moment of inertia and mass moment of inertia, the difference between them lies in the fact that the second moment of Area is used for the static areas, and used to determine the various types of stress, like bending moment and shear stress, while the torsional stress depends on the polar moment of inertia.
The second category expresses the resistance of bodies to angular rotations. the next slide shows the main differences.

The difference between the second moment of area about the x and y axes.
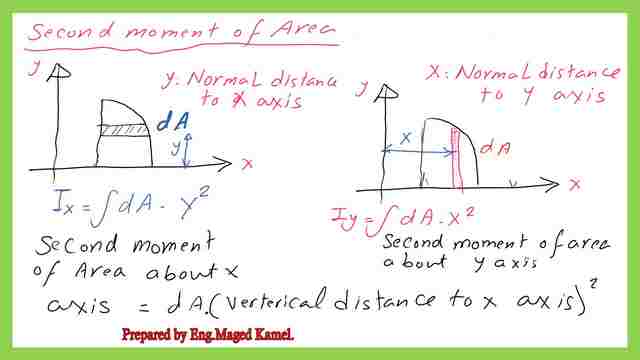
For the second moment of area, it can be estimated about x or y axes, We will introduce a strip and call that strip area dA.
If we are going to evaluate the inertia of the X-axis, we need to know the dimension of the normal dimension of the X-axis. The inertia about the x-axis is equal to the integration of d A * y^2, while, the inertia about the y-axis, as we can see, is equal to the integration of d A *x^ 2
X is the normal distance to the y-axis. In this regard, we are going to use a vertical strip, this strip, the area we call dA.
The integration symbol is the same as a summation of individual areas. In that regard, each area will be multiplied by its X component, but a symbol integration means that we are going.

Move this to strip multiplication by x^2. Starting from one point and ending at another point.
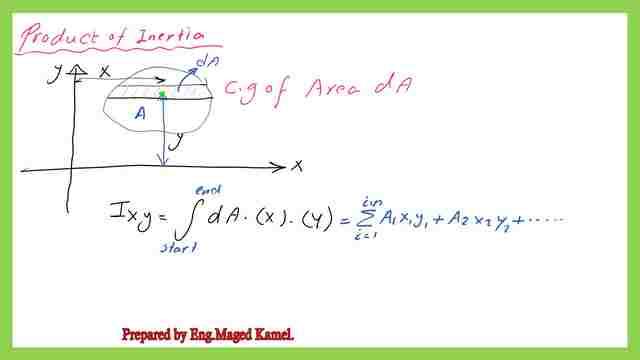
What is the product of inertia Ixy?
The next item will be the product of inertia, suppose we have a big area like this, where is the area we call A.
We will introduce only a small strip of area =dA from that strip, we are going to estimate the CG distance for both the x and y coordinates, for x is a normal horizontal distance perpendicular to the Y-axis, while y, is the normal distance perpendicular to the x-axis.
The expression for Ixy = the integration of dA* (xy), for that the strip, this = the summation, for example, Ax1y1+A2x2 y2, etc, where i=1 till i=n. In the end, instead of performing this task.
We will introduce only one small strip and start integration from our start point until our end.
What are the steps to estimate the inertia?
Number#1: Draw the element, to know what is the shape of that element, either a rectangle triangle, Trapezoidal, etc.
Number #2: Derive an expression for dA, by introducing the strip we will find out whether this is a horizontal or vertical strip.
Number #3 -Write the expression for the normal distances, for both X and Y, and make an interrelation between them. We need y if we are going to estimate the inertia at the x-axis, and the x distance if you are going to calculate the Iy, and of course, we need both if we are going to calculate the product of inertia.
Number# 4 Set the limits moving the strip, what point of start? until what point it will end, and in some cases especially in the triangle.
Number # 5-Perform the integration, after evaluating, we will get the moment of area value.

Parallel axes theorem proof for Ix.
There is a critical theory, which is called parallel axis theory, which we are going to prove for Ix, suppose we have two intersecting axes, namely x and y this is the area where we will estimate the moment of inertia by introducing a small area dA.
Deriving an expression for Ix.
We are going to estimate the moment of inertia, for example about the x-axis, we need the vertical distance from the CG of the dA small infinitesimal area dA.
This y can be estimated as, the sum of two components, the first component is called y1, and y1 is the vertical distance between the CG of the dA to the x’s, which is passing by the c.g.+ y bar, which we know, that the vertical CG distance from the external chosen x y.
If you’re going to write Ix= to the integration of dA*big distance Y^2, it can be equated to (y1+y bar)^2.
And if we’re going to estimate the I y for the moment of inertia about the y-axis, we are going to integrate d A x *x^2, as we are going to see. We will put it inside the bracket and will be multiplied by dA. Then Ix= the integration of dA*y^2+the integration of dA*2* y1*y bar+the integration of d A*y bar ^2. This first item, the multiplication of area *y1^2 will resemble the moment of inertia about the x ‘, which is the axis passing by the CG.

The moment of inertia about the x’ will resemble the inertia about the x ‘, which is the axis passing by the CG.
We will write as x ‘+ will resemble the moment of inertia about the x ‘, which is the axis passing by the CG which is an X’ passing by the CG, we are going to write as x ‘+ 2 *( y bar, being constant will come outside the bracket*, we left with dA*y1, the dA*y1 is the first moment of area, and since this is the axis about the CG.
As we know the first moment of area =0, this term will become 0 +A*Y bar^2. The moment of inertia = Ix’, about the axis passing by the CG, +A*y bar^2, in this regard, sometimes it is easy to estimate the moment of inertia at the external axis by subtracting the multiplication of the area by y^2.

This is the PDF used in the illustration of this post.
This is a link to the playlist for all videos for inertia.
For an external resource, Engineering core courses, the moment of inertia.
The next post: Moment of inertia Ix– for the rectangular section.

