The easy approach to permutation matrix-part 2.
We will continue in Permutation matrix-part 2 to discuss the various types of permutation matrices for the 3×3 matrix.
What is a permutation matrix P123?
This is the third arrangement of a permutation matrix (3×3) it is called P123, where there is a swap between row 1 to row 2 and also a swap from row 2 to row 3 and the last row r3 will be changed to row 1.
Such a matrix when multiplied by any other matrix will create a new matrix where the first row of the new matrix is the third row in the original matrix and the new second row is the first row of the original matrix. The third row of the new matrix is the second row of the original matrix.
A given example of the multiplication of a permutation matrix P123 with a matrix 3×3 is shown in the next slide image.


What is a permutation matrix P13?
In Permutation matrix-part 2, there is a fourth arrangement of a permutation matrix (3×3) which is called P13, where there is a swap between row 1 to row 3 and accordingly from r3 to r1, while the second row remains unchanged.
Such a matrix when multiplied by any other matrix will create a new matrix where the first row of the new matrix is the third row in the original matrix and the second row is the same as the second row of the original matrix. the third row of the new matrix is the first row of the original matrix.
A given example of the multiplication of a permutation matrix P13 with a matrix 3×3 is shown in the next slide image.



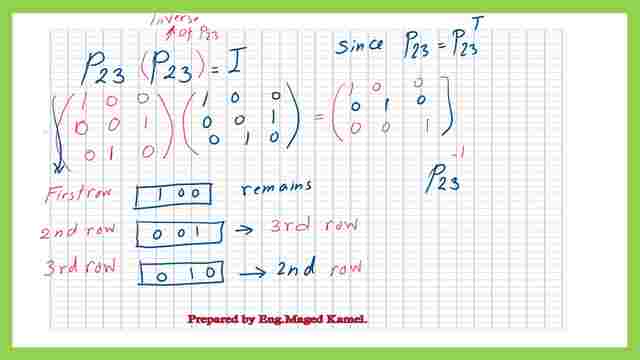
What is a permutation matrix P23?
In Permutation matrix-part 2, there is a fifth arrangement of a permutation matrix (3×3) it is called P23, where there is a swap between row 2 to row 3 and accordingly from r3 to r2, while the first row remains unchanged.
Such a matrix when multiplied by any other matrix will create a new matrix where the first row of the new matrix is the same as the first row in the original matrix and the second row is the third row of the original matrix. the third row of the new matrix is the second row of the original matrix.
A given example of the multiplication of a permutation matrix P23 with a matrix 3×3 is shown in the next slide image.



What is a permutation matrix P132?
In Permutation matrix-part 2, there is the last arrangement of a permutation matrix (3×3) is called P132, where there is a swap between row 1 to row 3 and also a swap from row 3 to row 2 and the second row r2 will be changed to row 1.
Such a matrix when multiplied by any other matrix will create a new matrix where the first row of the new matrix is the second row in the original matrix and the new second row is the third row of the original matrix. The third row of the new matrix is the first row of the original matrix.
A given example of the multiplication of a permutation matrix P132 with a matrix 3×3 is shown in the next slide image.


The multiplication of a permutation matrix by its transpose.
The transpose of a permutation matrix is the inverse of that matrix. The next slide image shows the operation of multiplying P123 by its transpose will create an identity matrix. The details of the multiplication of P123 by its transpose are shown.


Here is an example of multiplying P23 by itself will yield an identity matrix.

This is a link for the PDF file used in the illustration of this post and the previous post.
This is a link to the next post: Solved Example for LU decomposition-partial pivoting
This is the Omni calculator for estimating various items of linear algebra -LU Decomposition Calculator.
Link to Omni calculator-LU Decomposition Calculator.
Another calculator to use is Calculator for matrices.

