2- Easy introduction to Bisecting method for roots findings.

The bisecting method.

What is the bracketing method?

Introduction to bracketing method. The bracketing method is a  Numerical method, which represents two values of a function having opposite signs, the root will be in between. One example was solved first by using the analytical method as shown in the next two slides.

The root is the value of x when y=0, the bracketing method depends on two values for f(x), one of these two values will be negative and the other will be positive, the required root lies between these two brackets, that is why it is called bracketing method.

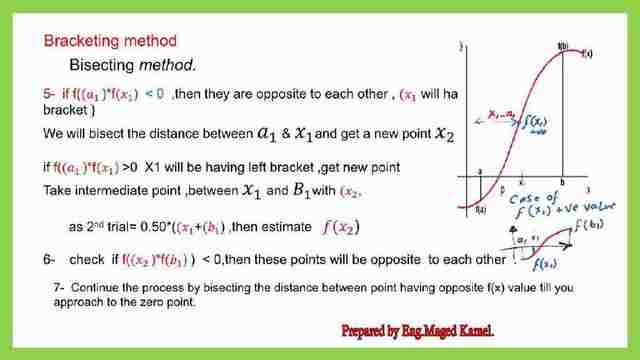
Bisecting method.

This is one of the bracketing methods, To find the root point, for f(x), the bisecting method, can be done by taking the average value of the horizontal distance between points of brackets, and then substituting it for the function, and determining whether the newly created point is left bracketed or right bracket.

Then perform a series of bisecting till the value of the function at a certain point approaches zero.

The different steps for the bisecting method are continued as shown In the next slide.
Let us trace the findings after using the bisecting method, when the new F(x) is either positive or -ve v, please refer to the next slide for an illustration.

Solved example for bisecting method.

This is a reminder of the analytic solution for the solved example. We will find the roots by using synthetic division for f(x)=x^3-6x^2+11x-6. We have three roots for this function. The details of the estimation are shown in the next slide image.

1-Now, let us refer back to our previous example and solve it by the Bisecting method. We have x=2.50 which gives a -ve value for F(x), then it is a left bracket. While  x=4 gives a +positive value for F(x), then it is the right bracket.

Take the average value of (2.50+4)=0.50*(6.50)=3.25.

2- Get the value for f(x), when x=3.25, so f(3.25)=2.5^3+11*2.5-6=0.7031. This is a new right bracket.
3- We make check that f(a)*f(b) is >=<0, we want to make sure that we have a negative sign, so (f(2.5)* f(3.25)=-0.375*(+0.7031)=-0.2636. The zero root is in between these two points.
Point (3.25) is a new right bracket.

4- Let us take the average between the left bracket and the right bracket points,(3.25,+2.50) as new x value x2=0.50*(3.25+2.504)=+2.875. check whether a right bracket or a left bracket.
5- Get the value for f(x), when x=2.875, so f(2.875)=2.875
2.875^3+11*2.875-6=-0.20508.This is a new left bracket.

6-We make check that f(a)*f(b) is >=<0, we want to make sure that we have a negative sign, so (f(2.5)* f(2.875)=-0.375*(-0.20508)=+0.076905.

The product is positive. A new Point (x=2.875) is a new left bracket. Then take the average between this last point(2.875) and our right bracket, x=4. the average is 0.50*(2.875+4)=3.0625.

7-Get the value for f(x), when x=3.0625, so f(3.0625)=3.0625^3+11*3.0625-6=+0.1369.This is a new right bracket.
8-We make check that f(a)*f(b) is >=<0, between the recent left bracket(2.875) and the recent right bracket(3.0625).

We want to make sure that we have a negative sign, so (f(2.875)* f(3.0625)=-0.03. the product is negative, Then the point (3.0625) is a new right bracket point.

Take the average between (3.0625,2.875)=2.968. Every operation is called an iteration. There are the details of iterations.

8-Get the value for f(x), when x=2.968 so f(2.968)=2.968^3+11*2.968-6=-0.06. This is a new left bracket.
7-We make check that f(a)*f(b) is >=<0, between the recent left bracket(2.968) and the recent right bracket(3.0625).
We want to make sure that we have a negative sign, so (f(2.968)* f(3.0625)=-0.01. the product is negative, Then the point (2.968) is a new left bracket point. After 5 iterations we get the value of x which will give an approximate solution.

This is the equation used for the number of iterations and the relative error.
Now for the error estimation, the number of iterations n should be bigger or equal to log10 (b₀-a₀)-log10(e)  of the error value the error, for a given error value of 0.001 divided all by (log 10(2).
So in our example, we have a₀=2.50 and b ₀ =4 for the errors of tolerance of value  0.001.

We can substitute like this n is bigger or equal to log 10 of (4 -2.50 )* (-3), that is the log value 10 of error 0.001 which is =-3 divided by log 10 of 2 is = ( – 0.16 6091) – 1-(-3))/0.301029 giving us 10.55, which can be approximated to 11.

Relative error equal to the (x new – x old) /  x new. For x value estimated for zero f(x).

This is the pdf is used in the illustration.

The next topic is the false position which is another numerical method for root findings.
This is a good external reference. Holistic numerical method.